ランダムフォレスト とは
ランダムフォレスト とは決定木(後述)を寄せ集めて実現される学習アルゴリズムです。ランダムフォレストを簡潔に表現すれば、「多数決のアルゴリズム」 と呼べます。
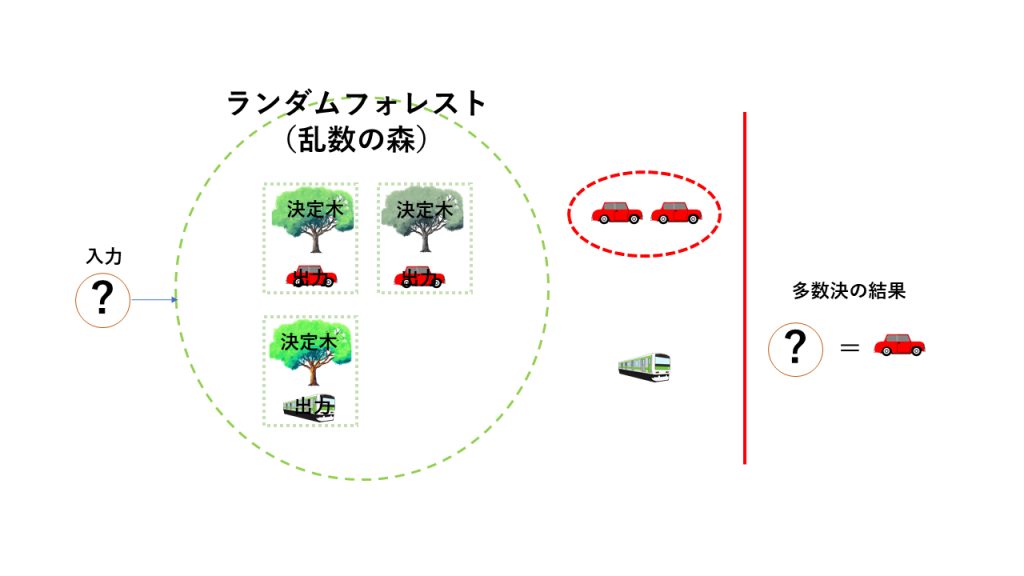
Random Forest ( ランダムフォレスト、乱数の森のイメージ図) アルゴリズムは比較的簡単で、決定木を適当に何本か作り、質問を投げかけます。答えた木の多数決により解が決まります。
例えば50本の決定木があったとして、40本の木がある質問に対してYesと答えた場合、この質問の回答はYesとなります。そして回答の正当性は80%で…という結果も得ることができます。ランダムフォレストの良いところは、木の数が確率で返答としても参考にできるところです。
以上のようにランダムフォレスト自体は解りやすいのですが、実装する上では決定木を理解することが必要です。
さて、今回は簡単に決定木のロジックを説明した後、実際にPythonで決定木を実装してランダムフォレストを作ってみます。有名人の顔のDB[2]を使って学習して男女判定のプログラムを作成してみます。
決定木とは
決定木は学習アルゴリズムの1つで、例えば質問してYes、Noで分岐していき、木構造を作成することで完成されます。
「完全に答えが出るまで分岐させ、これ以上分岐できないのであれば、そこで終わり」
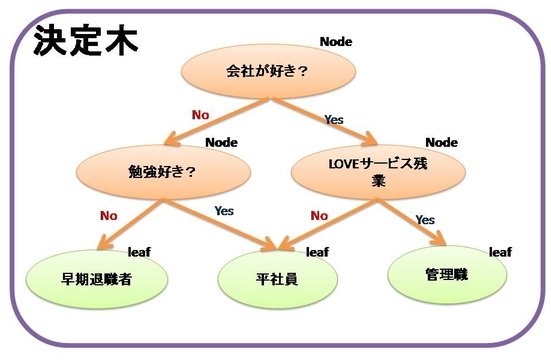
というアルゴリズムです。決定木のいいところは、分岐点を見ていくと、何故その判断に至ったのか論理的に理解しやすいところです。たとえば、以下のような決定木のとき、最終的な状態(leaf)はどのような項目(質問)により分類されたか、がわかるのです。
上記をみると役職の理由(平社員、管理職)が視覚的にわかります。学習後はこのような木ができて、なぜこうなったのかが理解しやすいのが決定木の良いところなのです。
ところで、決定木には分類木と回帰木という2種類があります。分類木はYes/Noや男女、暑い寒い、など2値をとる、あるいは分類するために用います。一方で回帰木は確率などの数値を取ることが出来ます。画像から年齢をとったり、スポーツ選手の成績から年俸を推定したり、結果が数値で表されるものに使われています。
今回は決定木で最も有名なCARTアルゴリズム(回帰木)を使って説明していきます。
決定木の作り方
「ある集合をなるべく偏りがあるように 2つに分断する。」
これをくり返していくことで木を作成していきます。偏りという概念には「情報エントロピー」を使います。
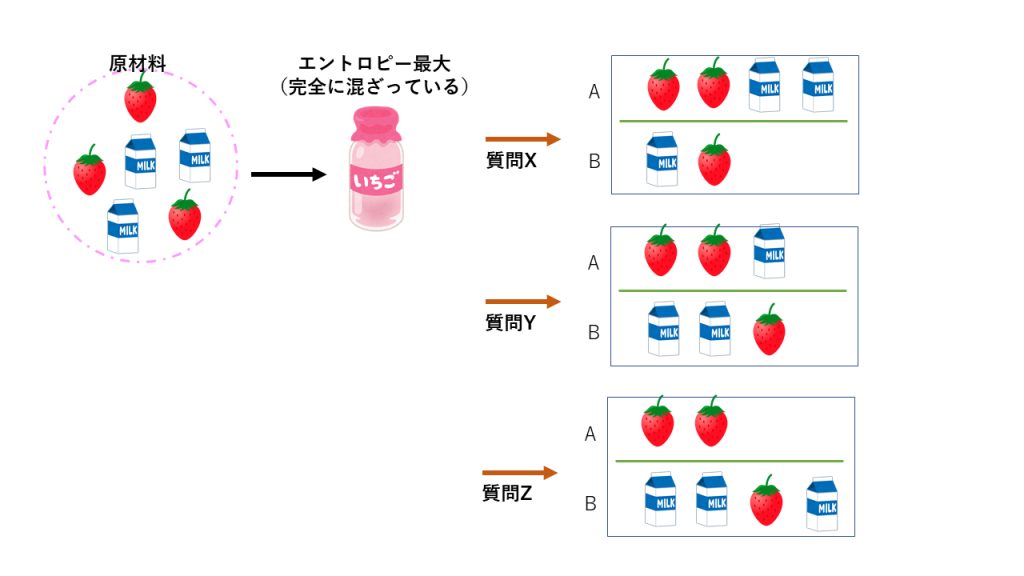
偏りとは、例えばYES、NOという回答が混ざっている状態から、YESとNOの2つの集合に綺麗に分けてやることです。他にも例えば「いちごミルク」から「いちご」と「ミルク」に偏ってわけたい(混ざった状態から、混ざってない状態に戻す)ことを偏りをつくるといいます。
Fig3. 偏りを作る例。質問Yの方が質問Xよりうまく偏りがある。質問Zは完璧ではないものの、結構精度が高く偏りがもとめられる。どれが、偏りが高いかを定量的に表すために情報エントロピーを利用する。 完全に混ざった状態はエントロピーが高い状態(乱雑な状態) であるといいます。逆に偏りがある状態をエントロピーが低い状態(偏った状態) と呼びます。なるべくエントロピーが低く低くなるような分岐状態(偏りがあるような分岐)を作っていくこと、これが決定木をつくる上で重要なことです。
偏るためには質問を用意します。質問は何でも良いですが、自分で用意する必要があります。先の例(Fig.2)であれば、今までの従業員の結果(役職)をもとに、彼らへの質問を用意しておくのです。質問の内容はたくさんあると思います。それこそ性別、勤続年数、宗教、出身地、出身校、目の色、頭髪、身長、体重などなど。(コンプライアンス的に引っかかるものもありますが、)こうした質問を用意しておいて、うまく分けることができたら(偏りを作れたら)良い質問だったということになります。
情報エントロピー 偏ったかどうかという判定に情報エントロピーを使うと言いましたが、それはとても便利だからです。情報エントロピーの数式は次の式となります。
情報エントロピーの式 : -\sum{P\log_2{P}} (1.1)
Pには数値が0−1までの数値が入ります。
情報エントロピーの値が元の集合の情報エントロピー値より低くならないのであれば、木はそれ以上枝を作りません。
情報エントロピーについて具体例で考える
先の式(1.1)を掘り下げましょう。男女の集合の中から、ある質問 をして「男」と分割した時のエントロピーを考えます。決定木では質問の後は必ず2クラス に別れます(グループA, グループBとする)。
グループAに男が存在する割合をP(x)とすれば、グループBに男が存在する割合は必ず1-P(x)となります。(2クラスしかないため)したがって男性側だけの情報エントロピーは、
P(x) * log_2{ P(x) } (グループAに男:GroupA(男))
と
(1-P(x)) * log_2{ (1-P(x)) } (グループBに男:GroupB(男))
この2つを足して、マイナスをしたのが、男性側の情報エントロピーです。
さて、男性がうまく分割しても、女性は分割出来ていない場合もあるかもしれません。女性にも男性と全く同じ質問 をして、女性側のエントロピーも求めます。グループAに女が存在する割合をP(y)とします。同様に2クラスしかないため1-P(y)がグループBに女性がいる割合です。
P(y) * log_2{ P(y) } (グループAに女:GroupA(女))
と
(1-P(y)) * log_2{ (1-P(y)) } (グループBに女:GroupB(女))
最終的にこの4つをすべてを足しこんで、マイナスした値-( GroupA(男)+GroupB(男)+GroupA(女)+GroupB(女) )が結果的な情報エントロピーとなります。(男女別情報エントロピーの合計,のマイナス)
今は男女になりましたが、昨今性別が増えています。性別が増えた場合も同様に足しこんでマイナスをすれば、最終的な情報エントロピーがでます。
上記でlogの底が2であることに注意してくだい。コンピューターで計算する際は変換公式によりlog_2{x}=\frac{log_e{x}}{fog_e{2}} を利用しましょう。
決定木は必ずノードで2つに分割するので、結局その場合のある要素の情報エントロピーは次の式となります。
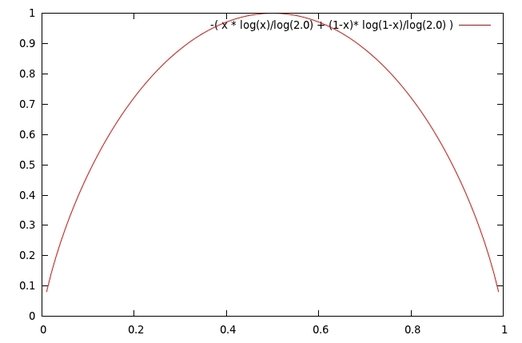
Entropy = - ( x * \frac{\log_e{x}}{\log_e{2}} + ( 1-x) * \frac{\log_e{1-x}}{\log_e{2} }) (2)
上記の情報エントロピーをGnuPlotで出力すると以下になります。
確率Pが0.5の時に上に凸の山なりのカーブを描きます。(最大値を示します)。0.5はランダムな状態(乱雑な状態)、分割がうまく行かなかったことを表します。ランダムであれば一番高い値となる、これが情報エントロピーです。情報エントロピーは前述の通り、低ければ低いほど偏りがあるという事になるのです。
こうして出来た決定木をあつめて、ランダムフォレストは作成されます。ランダムフォレストを作成する際の注意点は、同じ決定木を作らないようにすることです。 質問を違う順番でしたり、パターンを用意したり、様々な試行を行わなければなりません。多数決のアルゴリズムですので、それこそ多種多様な決定木があるほうが良いのです。
Pythonで 決定木 & ランダムフォレスト を実装
長くなってしまいましたが、いよいよPythonで実装してみます。今回は男女画像から男性と女性を判定する決定木を作っていき、それを用いてランダムフォレストを作ります。決定木のアルゴリズムの種類はCARTとします。
データセットが必要なのですが、顔画像のDB[2]からデータをダウンロードしてきます。この後、画像から顔をクロップして男女に分ける必要が有るのですが、既に私がやりましたので次のURLからfemale, maleのtarボールをダウンロードして解凍してください。github
Pythonでの実装の流れは次のようになります。
(下処理)2次元の画像を1次元にlist化する
(本処理)画像の輝度情報(つまり濃淡情報)を使って分割し、一番よく分割できたところを保存する
これだけです。それではまずはリスト化するところを説明します。
顔画像の一次元化
get_pixelsという関数を定義します。これは画像のファイルパスをもらってList化関数です。中ではカラー画像から輝度だけの画像にした後、ヒストグラム平滑化処理を行い、そして少しウィンドウを縮めてクロップしています。ウィンドウを縮める理由は髪の毛等ではなく、なるべく顔のパーツ情報から男女を判定してほしかったためです。
def get_pixels( path, w, h, crop_area = 0.86 ):
# 画像を開く
img = Image.open( path )
#画像サイズの取得
width, height = img.size
# マージンの比率を計算
margin_ratio = (1-crop_area)/2.0
#スタートの位置を計算
sx = (width * margin_ratio)
sy = (height * margin_ratio)
#輝度画像に変換
img = img.convert( 'L' )
# ヒストグラム平坦化処理(いらないかも)
img = ImageOps.equalize(img)
# 画像をクロップする
img = img.crop((sx, sy, width * crop_area, height*crop_area)).resize( (w, h), Image.BICUBIC )
# リストにして返す
return list( img.getdata() )
上記のリストを用いて学習していきます。
学習関数
あるsetをset1, set2に分割した際に、エントロピー(ランダムになっているかどうか)を計算します。ここでいうsetの構造は次のとおりになっているとします。
sets = [ ('M', [127,0,1,1, ....], ('F', [124,0,1,3, ....], ('F', [224,110,11,33, ....],,,,,,, ]
M, Fが書いてありますが、FemaleかMaleか判定するラベルです。その次の配列はlist化した顔画像の1次元の輝度情報です。さて、前の章で説明したエントリピーの計算は以下のとおりとなります。
def entropy( sets ):
# log2の関数を定義
log2 = lambda x: log(x) / log(2)
# ヒストグラムを取得する。ヒストグラムは頻度分布の事で、今回で言えば'F'と'M'が何個あるか計算する
def get_histogram( keys, sets ):
#{ 'F': 0, 'M':0 } という風に初期化
hist = dict( zip( keys, [0]*len( keys ) ) )
# keyから頻度分布を作成(1を足していくだけ)
for s in sets:
k, _ = s
hist[ k ] += 1
return hist
# ラベルの一覧を取得する。今回は'F'と'M'しか無いので、set([ 'F', 'M'])となる
unique_keys = set( [ _data[ 0 ] for _data in sets] )
# ラベルの一覧と、現在のデータを渡して頻度分布を取得する
histogram = get_histogram( unique_keys, sets )
# エントロピーの計算
ent = 0.0
for k in unique_keys:
p = histogram[ k ] / len( sets )
if p != 0:
ent = ent - p * log2( p )
return ent
エントロピーの計算方法は先程説明したとおりです。さて、これを用いていよいよ計算していきます。学習部分に関しては次のようになります。
# 輝度リストの中で、idx番目がvalueより高いかどうか判定
# ココの関数の定義によりある種分割が決まるから重要。ココは各々が思いついたアルゴリズムで実装すると良い
def split( sets, idx, value ):
set1 = []
set2 = []
for data in sets:
label, pixels = data
if pixels[ idx ] >= value:
set1.append( data )
else:
set2.append( data )
return [set1, set2]
# sets --> [('M':[輝度リスト]),('F':[輝度リスト]),('M':[輝度リスト]),('F':[輝度リスト]) ....]
# size --> 輝度リストの長さ
def train( sets, size ):
# 再帰関数として定義される。数が0であればその時点で終了する(分割が出来た)
if len( sets ) == 0: return 0
# ステップ数。輝度データをなめていくが、その飛ばしていく数。短いほうが遅くなる
step = 2
# 現在のエントロピーを計算する
current_score = entropy( sets )
# ゲイン値を使う。ゲイン値高いものが良い分割と判断する
best_gain = 0
best_criteria = None
best_sets = None
# 輝度配列の数だけぶん回し
for index in range( 0, size, step ):
for value in range( 256 ): # 輝度値は0-255までなので
# ある輝度値の条件に依って分割(後述)
set1, set2 = split( sets, index, value )
p = float( len( set1 ) ) / len( sets )
# gain値の計算
gain = current_score - p * entropy( set1 ) - ( 1 - p ) * entropy( set2 )
# 良かったgain値を保存
if gain > best_gain and len( set1 ) > 0 and len( set2 ) > 0:
best_gain = gain
best_criteria =( index, value )
best_sets=( set1, set2 )
# best_gainが更新されていれば、枝を生やす
if best_gain > 0:
ans_index, ans_value = best_criteria
true_branch = train( best_sets[ 0 ], size )
false_branch = train( best_sets[ 1 ], size )
return { True: true_branch, False: false_branch, 'index': ans_index, 'value': ans_value}
else:
return {'leaf': sets[0][0] }
エントロピーを使って分割しています。分割後はゲイン値を使って最も良かった分割を保存しておきます。そして、再帰的にドンドン分割していくのです。そして、分割ができなくなったら終わります。(Leafに到達)
ここで、splitという関数がありますが、自分でよく分割できそうだと思うような関数を書いてみましょう。今は単純に[index番目の濃淡値がvalueより高いか] で判断しましたが、画像の前後の上下の値を見たりするなど色々な工夫が出来る余地があります。
さて、これらを使ったmain関数は次のようになります。
import glob
import os
import random
from math import log
from PIL import Image, ImageOps
import uuid
import pickle
# 画像をランダムにサンプリング
def get_image_files( folder_path, picnum ):
return random.sample( glob.glob( os.path.join( folder_path, '*.jpg' ) ), picnum )
# female, maleフォルダより50個のファイルを取得する。
def main():
forest = []
num_tree = 30
# 木をぶん回す
for i in range( num_tree ):
print( f"building tree ... {i+1}/{num_tree}")
# 何枚の画像をフォルダからピックするか
num_pick = 150
female = get_image_files( './female', num_pick )
male = get_image_files( './male', num_pick )
# 画像サイズ 32x32にする
crop_size =32
sets = []
# データセット作成
sets += [ ('F', get_pixels( path, crop_size, crop_size ) ) for path in female ]
sets += [ ('M', get_pixels( path, crop_size, crop_size ) ) for path in male ]
size = 32 * 32
ret = train( sets, size )
forest.append( ret )
pkl_name = f"ret_{uuid.uuid4().hex}_size_{size}_picknum_{num_pick}_treenum_{num_tree}.pkl"
print( "dumped to --> ", pkl_name )
with open( pkl_name, 'wb' ) as fd:
pickle.dump( forest, fd )
これで決定木の学習、及びランダムフォレストの作成は終了です。一本の決定木からは次のようなデータが出てきます。
{True: {True: {True: {‘leaf’: ‘M’}, False: {‘leaf’: ‘F’}, ‘index’: 428, ‘value’: 196}, False: {True: {True: {‘leaf’: ‘M’}, False: {True: {‘leaf’: ‘M’}, False: {‘leaf’: ‘F’}, ‘index’: 552, ‘value’: 162}, ‘index’: 606, ‘value’: 137}, False: {‘leaf’: ‘M’}, ‘index’: 326, ‘value’: 157}, ‘index’: 910, ‘value’: 198}, False: {True: {True: {‘leaf’: ‘F’}, False: {True: {‘leaf’: ‘M’}, False: {True: {‘leaf’: ‘M’}, False: {‘leaf’: ‘F’}, ‘index’: 0, ‘value’: 220}, ‘index’: 78, ‘value’: 102}, ‘index’: 710, ‘value’: 115}, False: {‘leaf’: ‘M’}, ‘index’:212, ‘value’: 92}, ‘index’: 358, ‘value’: 92}
これは、辿るマップを示しています。今回は濃淡配列のindex番目の値がvalueより大きければ、Trueをたどっていき、そうでなければFalseをたどります。これは、split関数で定義した内容と同じである必要があります。最後にLeafに有る値が決定木に依って判定された値です。
注意が必要なのが、今回は画像をCropして、ヒストグラム平滑化処理をしています。検証する画像にも同様の処理をする必要が有る ことについて、注意しましょう。
検証
検証用のコードは次のとおりです。
def tree_result( node, data ):
if 'leaf' in node: return node[ 'leaf' ]
index = node[ 'index' ]
value = node[ 'value' ]
cond = data[ index ] >= value
return tree_result( node[ cond ], data )
def validation():
with open( 'ret_a239b96f07d6443c851582866e4b7724_size_1024_picknum_150_treenum_30.pkl', 'rb') as fd:
forest = pickle.load(fd)
# print( forest )
num_pick = 100
female = get_image_files( './female', num_pick )
male = get_image_files( './male', num_pick )
crop_size =32
sets = []
# データセット作成
sets += [ ('F', get_pixels( path, crop_size, crop_size ) ) for path in female ]
sets += [ ('M', get_pixels( path, crop_size, crop_size ) ) for path in male ]
passed = 0
failed = 0
for d in sets:
count = 0
label, pixels = d
for tree in forest:
ans = tree_result( tree, pixels )
if label == ans:
count += 1
if count > len( forest )/2:
print( "Passed" )
passed += 1
else:
print( "Failed" )
failed += 1
print( 'correct ratio --->', passed / ( passed + failed ) )
上記の通り、validation関数内でpklファイルを指定して読み込みます。今回は、私の方で検証した結果は正答率82%という結果を得ることが出来ました。何もしていない濃淡情報だけでここまで出ました。顔画像のCropも適当です。
回転や縮小に堅牢な特徴量を用いいればもっと精度は向上するでしょう。
さて、ご存知のとおり特徴量を考えるような時代は終わりつつあります。それはGANなどの登場によりコンピューターが自動的に特徴量的なものを学習時に作り出す時代になっているからです。昔はみな回転や縮小に不変な特徴量を考えるのに四苦八苦したものです。
確かに特徴量を考える時代は終わったかもしれませんが、以前顔画像ではなく統計情報を解析したいときなどには未だに強力な武器です。データアナリストをめざすのであればぜひ一度実装して楽しんでみてください。
最後に
実は、決定木ではかならず2分割されると書きましたが、実際にはエントロピーを使うと3分割、4分割も出来ます。ただ、ランダムフォレストを使う場合あまり意味がないものとなるでしょう。解析や判断も複雑になるため、基本的には2分割の決定木を使ったランダムフォレストで十分な精度が出ます。
実は、ランダムフォレストは非常に強力です。これ一本で(何本もありますが)本当に様々なことが出来ます。機械学習の仲間と話しますが、これだけでもいいと思うくらいです。
回帰木は連続した値を扱えるところが素晴らしかったのですが、木を作るのに時間がかかるデメリットやオーバーフィッティングのデメリットがあります。ランダムフォレストをつかえば、何本の木が返答したというような確率を使うことができるので、たとえ分類木を使ったランダムフォレストでも、連続したデータも扱えるようになります。
さぞかし回帰木をつかったランダムフォレストは更に精度が高くなるのでは!?と思うかもしれませんが、実際にはあんまり変わりません。よくよく考えれば、回帰木のランダムフォレストって、重回帰分析の重みの平均みたいなイメージになるのかなぁ、とおもってしまいます。
参考サイト
[1]https://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%83%80%E3%83%A0%E3%83%95%E3%82%A9%E3%83%AC%E3%82%B9%E3%83%88
[2]http://vis-www.cs.umass.edu/fddb/index.html
[3]https://axon.cs.byu.edu/~martinez/classes/778/Papers/GP.pdf
おすすめ記事