Matrix Factorization(MF)

はじめに

Matrix Factorization(MF)について解説していきます。

現在世にある推薦システムは殆どMFをベースに作られているといっても過言ではありません。Simon Funkという人がNetflix Prizeに応募するために開発し、とても話題になりました。SVDを用いて推薦システムを構築したのですが、あるトリックを用いたSVDであったため、中のエンジンはFunk-SVDなんて言われたりしています。他にもNMFを利用したりSVD++など改良が進んでいますが、メインのやり方は本稿の説明でわかるかと思います。

何故SVDを改良する必要があったのかと言えば、SVDは疎でない（スッカスカでない）行列の解析には素晴らしく良い結果をもたらしていました。しかしながら、商品や映画の推薦となると、全てのユーザーが全てのアイテムを推薦している訳はありません。実際に映画のレーティングの行列を作ると95%のがNaN（未評価）であったということからも、推薦のもとになる行列はとても疎な行列です。この状況を改善しようとした試みがFunkSVDだったというわけです。

概要

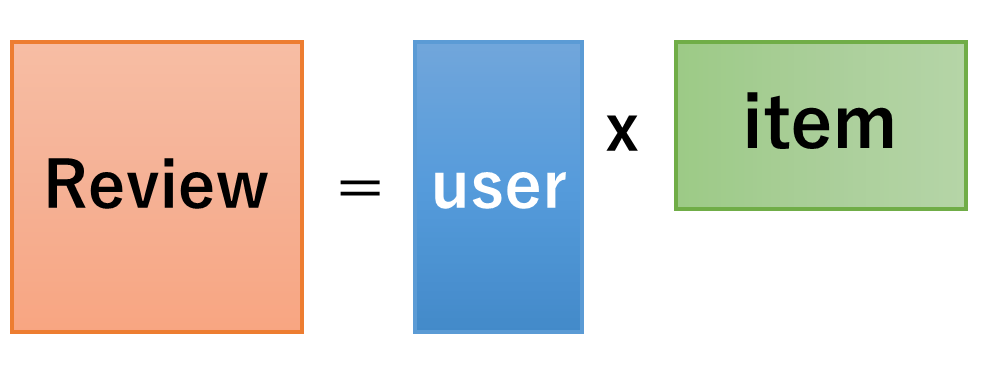
Matrix Factorizationの流れを説明します。次のようなレーティングマトリックスを２つ(Item & User )に分けるものです。他のサイトと差別化するために、本ブログでは一番わかり易い表ベースの解説をします。今、以下のようなレーティングマトリックスがあったとします。

	Movie 1	Movie 2	Movie 3	Movie 4
User 1	5	NaN	8	3
User 2	7	7	NaN	4
User 3	NaN	6	7	7
User 4	10	NaN	NaN	NaN

上記の行列を２つの行列q, pに分ける事をMFでは行います。

\hat{r}_{ui} = q_i^Tp_u

$\hat{r}$ は推定されたレーティングという意味し、実際のレーティングは $r$ とします。

$p_u$ はユーザー、 $q_i$ はアイテムを表す行列です。今回の目的は、ユーザー特徴量行列とアイテム特徴量行列をつくり、それらを掛けると元の行列にする事です。

これは実際のレーティング $r$ と推定レーティング $\hat{r}$ の2乗誤差を最小にするというな行列を分解する,という意味でもあります。式で表せば次のようになります。

minimum( p,q ) \sum_{u,i\in K}(r_{ui}-q_i^Tp_u)^2

p, qを作る

ユーザ特徴量行列 $p$ 、アイテム特徴量行列 $q$ は今は未知なので適当なランダム値で埋めてやります。

p=

	Factor 1	Factor 2	Factor 3
User 1	1.4	0.4	-1.2
User 2	1.3	1.5	-0.3
User 3	0.8	0.1	0.6
User 4	-0.7	0.5	1.1

q=

	Movie 1	Movie 2	Movie 3	Movie 4
Factor 1	0.6	0.5	1.3	-0.5
Factor 2	-1.1	-0.4	0.7	1.3
Factor 3	1	0.3	0.5	-0.1

さて、説明のために、User1のMovie3に注目します。

実際の評価 $r$ はレーティングマトリックスをみてみると”8″でした。

ユーザ特徴量行列p（青）ではUser 1は[1.4, 0.4, -1.2]

アイテム特徴量行列q（緑）のMovie3は[1.3, 0.7, 0.5]

です。推定された評価 $\hat{r}$ は[1.4 * 1.3 + 0.4 * 0.7 + 0.5 * -1.2 ] = 1.6となります。なお、算出しなくてもいいのですが２乗誤差はは $(8 - 1.6)^2=40.96$ となりました。

更新処理

誤差を元にp, qの値を更新します。p,qの行列から参照した要素は次のとおりでした。

From p

1.4

0.4

-1.2

From q

1.3

0.7

0.5

新しい特徴値は次の計算式を用いて求めます。

p_i = p_i + 2 \alpha ( r - \hat{r} ) q_i

q_i = q_i + 2 \alpha ( r - \hat{r} ) p_i

ここでαは学習率と呼ばれ、0.1くらいにするケースが多いです。これに習ってpの最初の要素を計算してみると、次のようになります。（ $p_0$ は1.4, $q_0$ は1.3を指します）。何故この更新式になるかは[2]を参照ください。

1.4 + 2 \times 0.1 \times ( 8 - 1.6 ) \times 1.3 = 3.064

出た値を用いて $p_0$ の値を更新します。

3.064

0.4

-1.2

同様にp, qの残りに対しても更新処理を行います。なお、qの更新式ではpの値も使いますが、既に更新された値を使います。

上記例では $p_0$ の値は3.064になりましたので、 $q_0$ を求める際には、新しい数値を使います。あとは繰り返し処理を繰り返し行い、すべてのp, q行列を更新していきます。以上となります。

これを学習データを用いて適当に取ってきた値で特徴量行列を更新していきます。

ちなみに本当の評価 $r$ がNaN値であれば重みの更新処理をしなくても構いません。（というかしません。）。これがNaN値を考慮したSVDであると言える理由です。

重み更新は、ニューラルネットワークなどではおなじみなのですがStochastic Gradient Descent (SGD)：確率的勾配降下法と呼ばれています。ランダムに（確率的に）適当な値を引っ張ってきて、重みを更新している（勾配をもとに、2乗誤差を低くするように降下させている）からです。差分がゼロ（微分がゼロ）になれば、最適解に到達したと言えます。

なぜ特異値分解：SVDと呼ばれるのか

今までの操作のどこが特異値分解なのでしょうか。

特異値分解とは、ある行列をエラーを最小とするように２つに分割する操作でした。今回分割する際に行ったことは2乗誤差が最小になるように分割していく操作です。SVDはもともと最小二乗近似を得る方法とも言えます。実際に開発者のFunkも自身のブログで次のように述べています。

Singular value decomposition is just a mathematical trick for finding those two smaller matrices which minimize the resulting approximation error–specifically the mean squared error (rather convenient!).

さて、大まかな説明はこれで終わりなのですが、更にいろいろな工夫をすることで精度が高くなります。SVDのかわりにNMFを使うことだったり、今回はマトリックスを分割する際のエラーの計算方法として単純にpqに分けるようにしましたが、実際に精度を出すためには正則化したり、バイアス項を突っ込む必要があります。

さらなる改良

正則化

結局重みは次の式を最小化するということでした。

minimum( p,q ) \sum_{u,i\in K}(r_{ui}-q_i^Tp_u)^2

ここで上記式に正則化をします。（過学習を防ぎ、一般的に使えるようにするためにペナルティ項をおく）

minimum( p,q ) \sum_{u,i\in K}(r_{ui}-q_i^Tp_u)^2 + \lambda (\|q_i\|^2 +\|p_u\|^2)

最初の項目に $\lambda (\|q_i\|^2 +\|p_u\|^2)$ をおいただけです。この意味ですが、1つの映画を酷評したユーザーがいて、その映画以外は評価していなかったとします。すると、このユーザーから他の映画へのすべての評価が非常に低くなります。この正則化をおけば、例えば $q_i$ に大きな値を与えることを抑制することになります。

バイアス項

推測されるレーティングは次の式でもとまるものでした。

\hat{r} = q_i^Tp_u

ここに３つのバイアスを加えます。

$\mu$ 全アイテムの平均レーティング
$b_i$ アイテムiの平均レーティングから $\mu$ を引いたもの
$b_u$ はユーザーuの平均レーティングから $\mu$ を引いたもの

最終的に、レーティングの式は

\hat{r} = q_i^Tp_u+\mu + b_i + b_u

となります。そして、こちらにも正則化項をいれます。

minimum( p,q ) \sum_{u,i\in K}(r_{ui}-q_i^Tp_u)^2 + \lambda (\|q_i\|^2 +\|p_u\|^2+b_i^2+b_u^2)

これが最終的なSVDの式となります。長くなりましたが、これでMFの説明は終わりとなります。

最後に

その他、NMFやSVD++など、エンジンを変えて更新式を実行したい場合は、次のURLに詳細に書かれています。[1]

もしNMFによる実装方法などを記事化してほしい方がいれば、コメントをいただけますと幸いです。

索引

[1]https://surprise.readthedocs.io/en/stable/matrix_factorization.html#surprise.prediction_algorithms.matrix_factorization.SVD
[2]Web Data Mining. Exploring Hyperlinks, Contents, and Usage Data
Authors: Liu, Bing

投稿者: 等々力康弘

画像処理エンジニア。組み込みソフト出身。株式会社モルフォにてR&D部門、主に機械学習業務に携わり、顔認識＆顔検出のアルゴリズム開発に従事。国内特許数件、国際特許１件。モルフォ社退社後、株式会社Dynaptico創業（CEO)。アメリカ人、スウェーデン人と３名とフードデリバリーサイトmaishoku.comを立ち上げる。社長業の他、開発業務においてバックグラウンド関連全般(Djangoを用いいたバックエンドサーバ＆APIサーバーの作成、リバースプロキシなどの負荷分散サーバ関連、OCRプログラムの作成、CISCOルータの管理, 、seleniumを用いたテストサーバーの構築、Androidアプリの開発等々）に携わる。 2019年DynapticoのCEOを辞職。 2020年2月にComputer Scienceに特化した株式会社OctOpt創業。 OSはUbuntu。Appleが苦手。Swiftのバージョンアップ対応とか死ぬほど嫌い。 Python/C++/C Twitter: @rocky_house シフト自動調整スケジュールサイトをVue.js+graphene djangoで構築. https://www.allshifter.com 等々力康弘のすべての投稿を表示