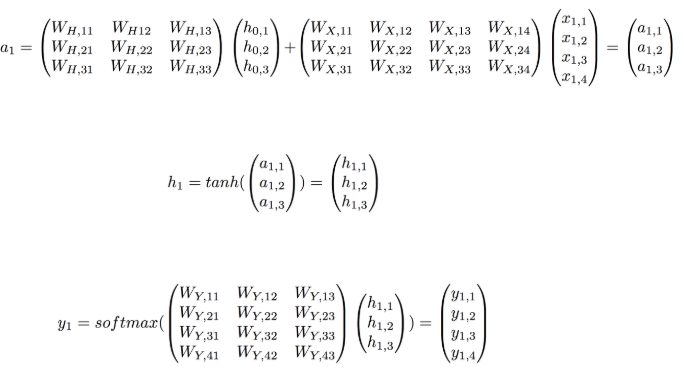Transformer (トランスフォーマー)のアルゴリズムについて解説します。Transformer はNLP界だけでなく画像処理界でとても話題となりました。
2015年Sequence2Sequence でNLP界隈は盛り上がりましたが、2017年にAttention all you needを発表し、 Transformerという新しいモデルが生まれ、学習時間面と精度でSeq2Seqを抜き去り更なる盛り上がりを見せたのです。
TransformerはDeep Learning 研究の中でも非常に大きなブレイクスルーを起こした技術の1つとなりました。(TransformerもAttentionというSeq2Seqで注目された技術をつかっているため、全ては必然で誕生してきた技術という感じもします)個人的には2021,2022、2023年の最新技術にふんだんに使われており、この技術がなくしては今のChatGPTなどもありません。
最新の翻訳技術で有名な所はTransformerの派生、改良版みたいなものです。2018年末にはGoogleのBERT、2020年4月にOpenAIからGPT-3などが発表されていますが今回説明するTransformerの技術が礎となっています。
画像処理に関しても、Stable diffusionのエンコーダーではTransformerが使われていますし、入力には単眼カメラによる深度マップが必要なのですが、それを作成するにも、MiDas などのDPT(Dense Prediction Transformer)アーキテクチャベースが使われるのですが、名前の通りTransformerが使われています。
こうした最先端の技術の礎となっているTransformerについて、本ブログではソースコードをメインに解説していきたいと思います。
Transformer
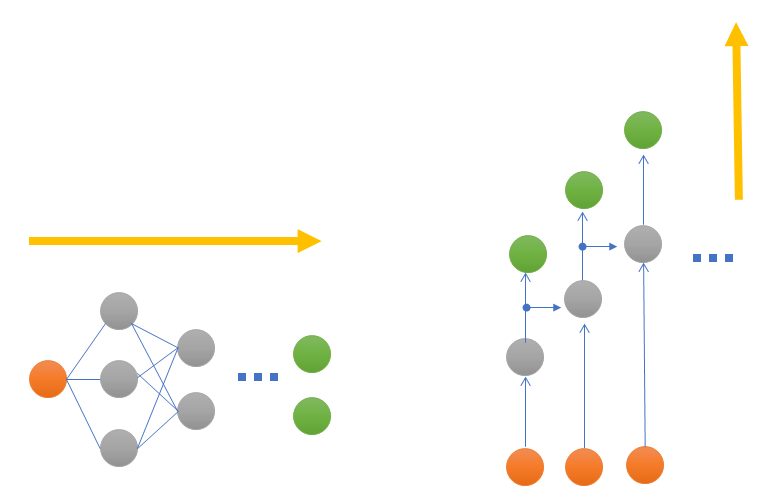
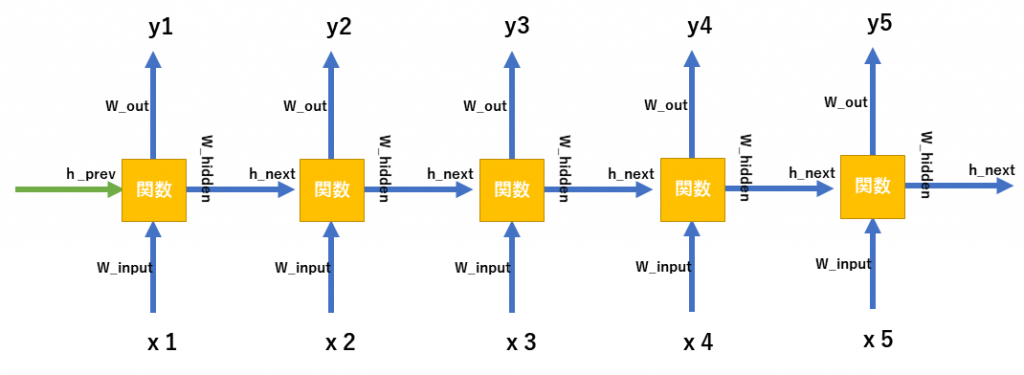
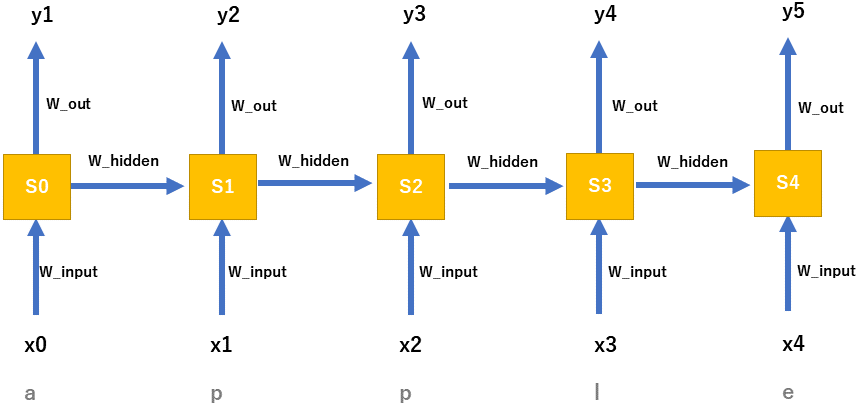
トランスフォーマーが産まれたのは、雑に言えばSeq2Seq(+Attention)を並列化して高速に学習したかったからです。(Seq2seq+Attentionの概略については、後ほど説明します)
並列化と聞いてまず思い浮かぶのがCNNなどコンボリューションです。並列処理が得意なGPUに向けて行列演算に落とし込めば並列化が見込めます。しかし、Seq2Seq+Attentionはバケツリレー形式で情報を運んでいる(前の入力に対しての処理をしている)ので並列化はできません。
そこでTransformerでは、Seq2SeqのAttentionを、self-attention層という独立して計算する層をつくり、行列演算を用いて並列化を実現しました。
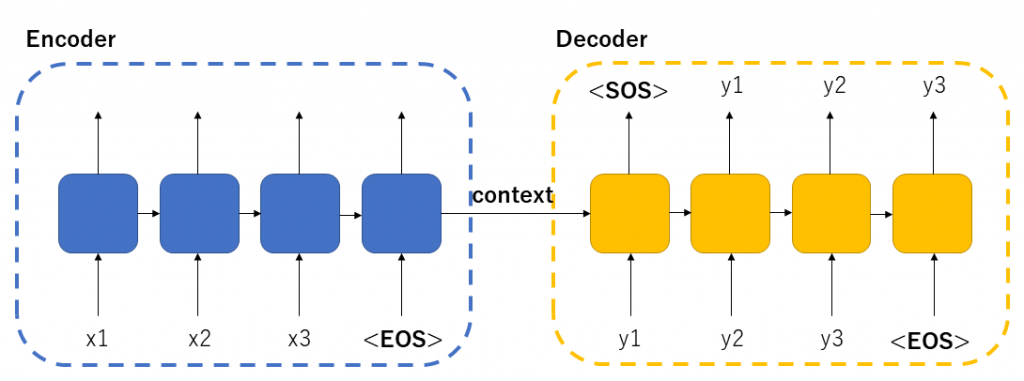
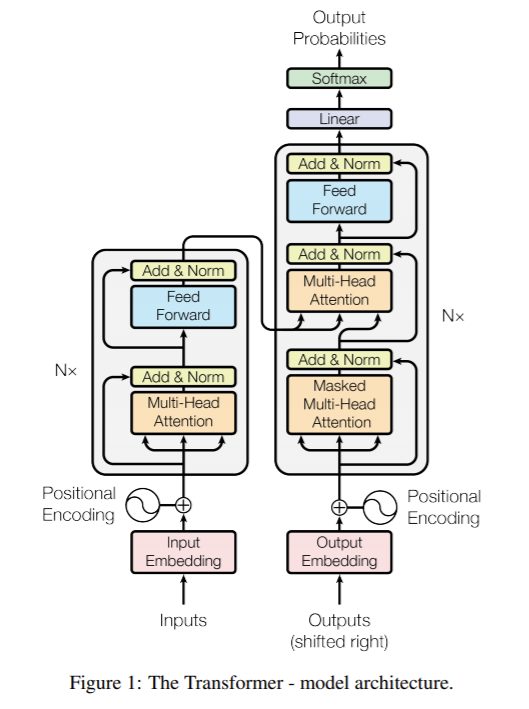
Seq2Seqでは全体でAttentionを実現していましたが、Transformerではattention層という単位に落とし込んで実現しています。下記に簡単にTransformerの全体図を示します。
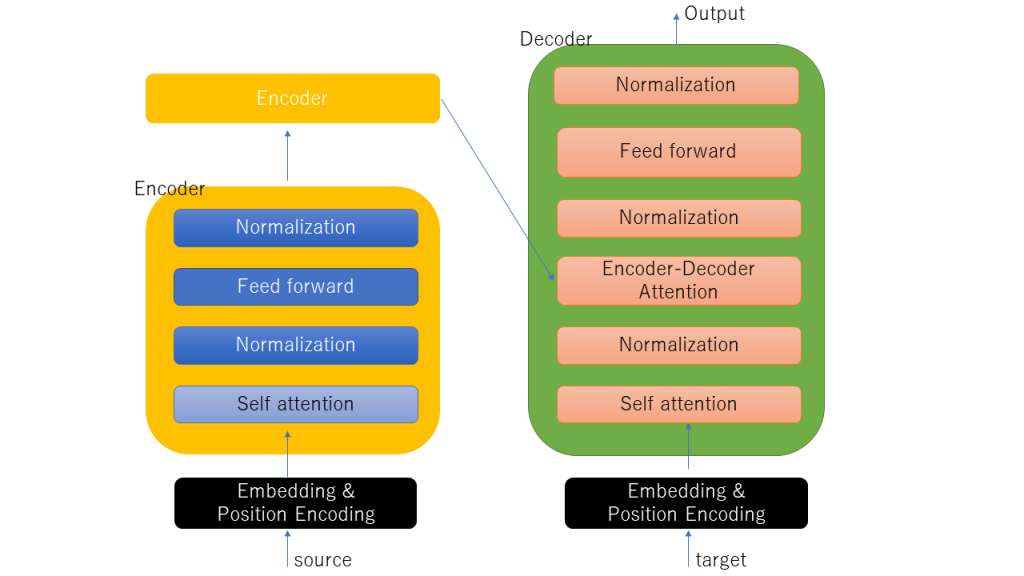
右側DecoderのOutputでは最後にSoftmax処理が入る。Encoder,Decoderで、Self-attention層があり今までのSeq2Seqとは様相が異なる形がわかる
上図がTransformerの全体図になります。Encoder部とDecoder部の2部構成であり、これはSeq2Seqと同じです。また、Encoder,Decoderとも多段で接続(オリジナルの論文では6段)で構成しています。
Transformerでの肝はずばりSelf-attention層となっています。Self-attention層は同じセンテンス内の単語群が、翻訳したい単語にどれだけ影響しているかというものを検出します。
Transformerを構成しているEncoderとDecoderともに、Self-attetion層やNormalization層など同じ層を使って構成しています。Decoderにしかない特徴的な層があり、それは、Encoder-decoder attention層となります。後ほど説明しますが、Self-attention層とやることは同じなのですが、Encoder側からバイパスしてもらう特徴量(最後の段のEncoderからの入力)を用いて2つの特徴行列(Key, Valueを生成する行列)を学習し、Self attentionを行っています。これにより入力のどのパーツに注目するべきかを考えることができます。全てのDecoder群のEncoder-decoder attention層では、最後のEncoderが出力した特徴を使うことになります。それでは各層の流れを説明していきます。
Transformer 各層の説明と流れ
Transformer内部のEncoder, Deocder内部の層がどのような処理をしているかを記載していきます。それぞれの層の説明、特にSelf-attentionはなかなか濃ゆいと思うのでじっくり理解していってください。
Encoder、Decoderそれぞれでは
- 事前処理Embedding
- 事前処理Positional Encoding
- self-attention層( + Encoder-Decoder attention層( decoderのみ ) )
- Normalization層
- Feed forward層
というような処理を順次行っています。それぞれの処理について説明していきます。
1.【事前処理】Embedding処理
Embeddingは文字の埋め込みを行います。Word2Vecの様な処理です。具体的には例えば512次元のベクトルに単語を変換します。例えば I am an studentであれば、
I = [ 0.1, 0.2, 0.03, 0.78 …. 0.04 ], am = [ 0.41, 06., 0.033, 0.378 …. 0.3 ], an = [ 0.41, 0.52, 0.073, 0.5678 …. 0.34 ], student = [ 0.81, 0.62, 0.023, 0.478 …. 0.54 ]
のように一つ一つの単語に対してベクトルに変換をします。pytrochではEmbeddingは関数一つで実現でき、上記例では512次元のベクトルに変換するのにembedding = nn.Embedding(4, 512)としておき、embeddingを呼ぶことで実現できます。Embeddingの方法やアルゴリズムについては[10]を参照してみてください。要するにここで文字列をベクトル化してやって学習するようにするのです。
2.【事前処理】Positional Encoding(PE)処理
Positional Encoding (PE)は順序の定義を行います。今回のTransformerでは行列演算により並列化し従来よりも高速に計算をするという目的がありました。並列に行列計算を行うため、文章の単語に対して順序(もとにいた位置)を考慮させる必要があります。Seq2Seqのようにバケツリレーではないので、バラバラにしてももとの位置が解るような情報量を与える必要があります。
順序でいえば、例えば0,1,2,3とindex値を割り振ればいいと思うかもしれませんが、文字数が大きくなると、値も大きなってしまいます。そもそも-1〜1の範囲で正規化して学習するため整数のindex値は相性が悪そうです。じゃあ正規化をすれば良いのではないかと思うのですが、今度は別の問題が発生します。例えば、5文字のセンテンスがあったとして0.8は四番目の文字を意味します。所が10文字の0.8は8番目になります。つまり、同じ値に場所が違う問題が発生します。
では、文字列の次元を固定(例えば512次元)して、割り振ればいいと思うかもしれませんが、ほとんどの文章は20単語くらいでしょう。そうすると、ものすごい無駄な空間(20次元以降の情報は使われることは殆ど無い)となります。
さて、こうした問題を解決したのが余弦、正弦を使った順序の定義です。数式は次のとおり表されます。
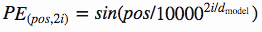
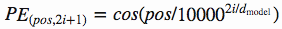
上記式を例えば128次元(d_model)と仮定すると、以下のような画像となります。[11]
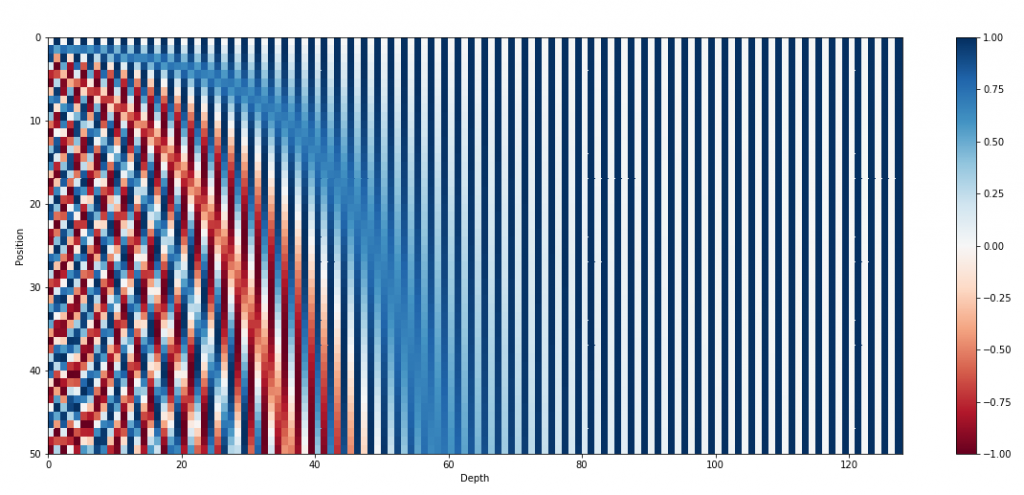
Embeddingしたinputを、このPositional Encodeing の値と足し込めたものをインプットとして利用します。疑似コードを書くと次のとおりです。
x = Embedding( input ) + PositionalEncoding( input )
上記のように簡単に書くと足しこむだけです。実際に疑似コードでなくPyTorchで実装を書くと以下のような実装になっています。
import torch.nn as nn
import math
import torch
class PositionalEncoder(nn.Module):
def __init__(self, word_num, dim ):
super().__init__()
self.dim = dim
# word_num行, dim列のゼロベクトルのpe(positional encoding)の作成
pe = torch.zeros(word_num, dim)
for pos in range(word_num):
for i in range(0, dim, 2):
pe[pos, i] = math.sin(pos / (10000 ** ((2 * i)/dim)))
pe[pos, i + 1] = math.cos(pos / (10000 ** ((2 * (i + 1))/dim)))
# 行列[ [ ...],[....],,, ]を更に囲む(Tensor化)
pe = pe.unsqueeze(0)
def forward(self, data):
data = data * math.sqrt(self.dim) # ちょっと値を大きくしてやる
seq_len = data.size(1) # dataのワード数を取り出す
data = data + torch.tensor(self.pe[:,:seq_len], requires_grad=False) # 足し込む処理
return data
3.Self-attention層
そもそもAttentionとは
Transformerを学ぶ前にTransformerの目玉の一つでもあるAttentionという技術はどういう技術か紹介します。
「Attention」は注目という意味となります。つまるところAttentionとは、入力の注目する部分を見つける!ということになります。
画像処理で言えば、学習時に犬だけに注目して処理したもの(犬を全景処理で切り出したもの)と、画像全体で処理したものを使っての学習では、効率や結果が変わりそうです。犬だけに注目したい!というのがAttentionという技術となります。この技術は文章にも適用ができ、例えば翻訳の部分では翻訳する際にどこにまず注目した方が良いのか、や、文章の単語同士の関わりの指標みたいなのを抽出することが出来るようになるのです。
言葉で説明してもわかりにくいかもしれません。この技術をYoutubeで15分で紹介している方が居ました。素晴らしく解りやすいので、是非ご覧になってください。
Attentionは対象物のみに集中する、という意味で逆に言えばそれ以外を無視するという雑な言い方も出来ます。実際に我々の脳でも同じことをやっています。例えば集合写真で人数を数えてくれって言われたら、頭の数を数えてほかは無視するようにすると思います。このように、人間と同じようなことをするという方法がAttentionという方法です。
Seqence to sequence with the Attention
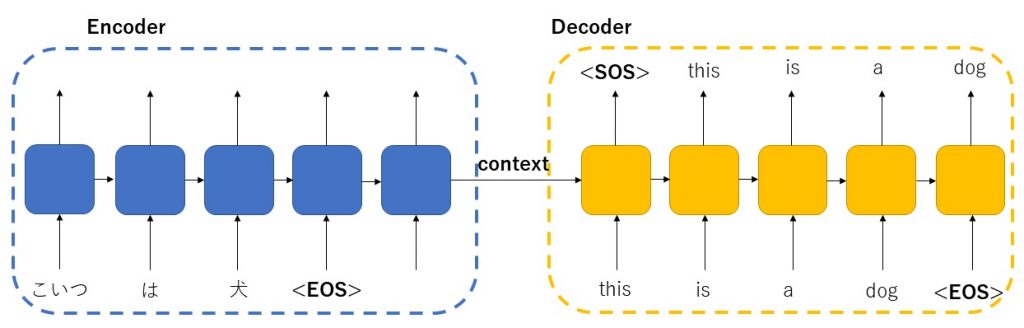
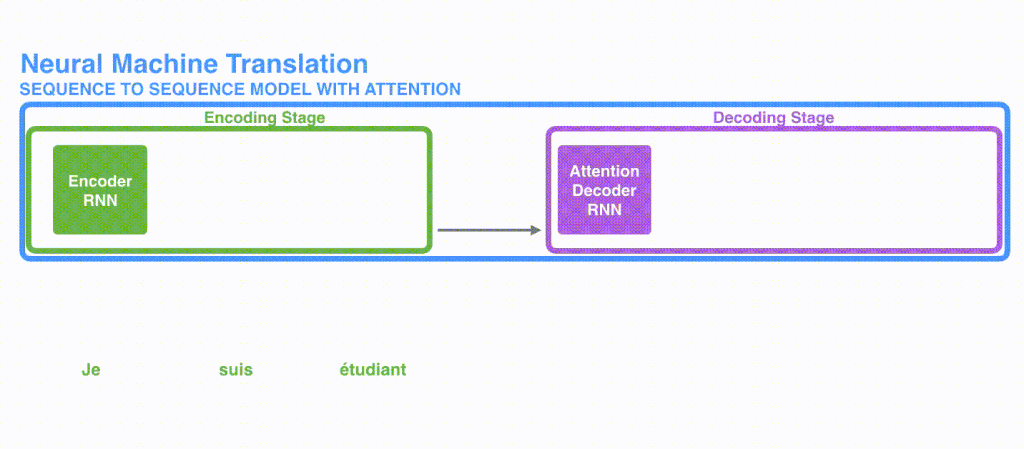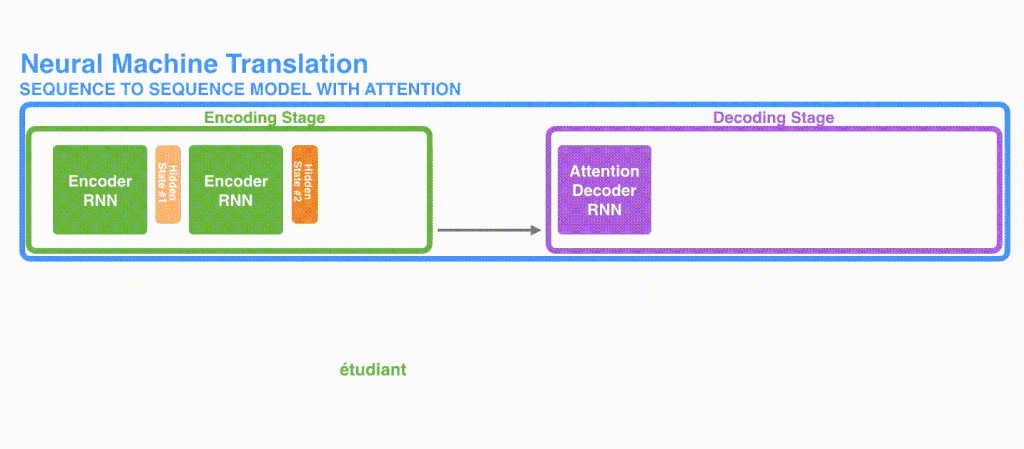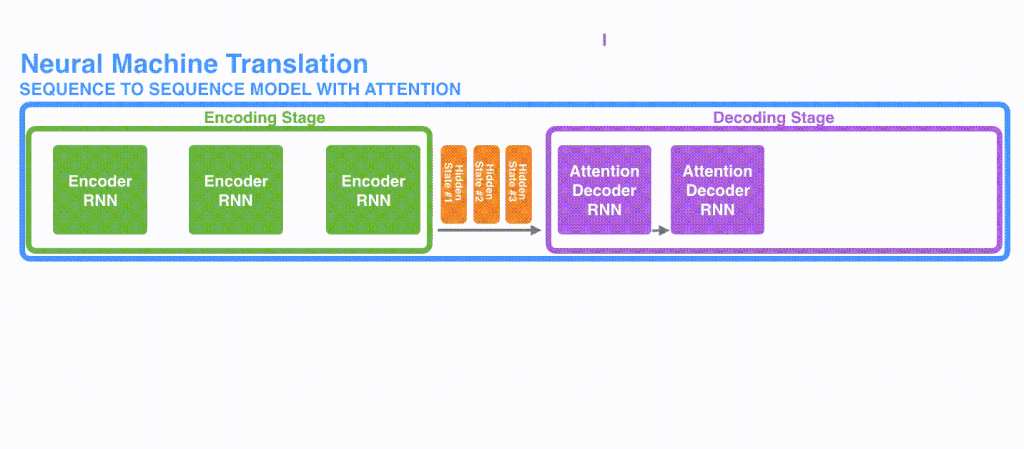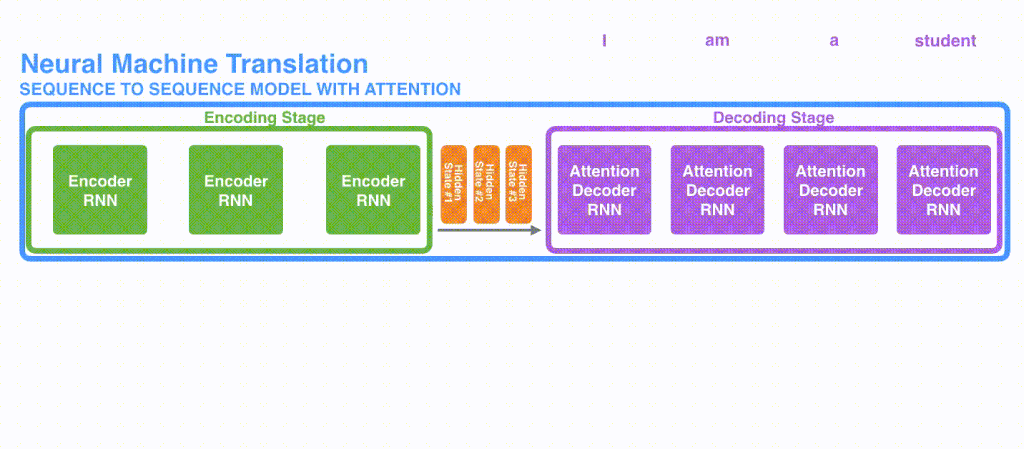
実際のAttentionの使われ方をSeq2Seqモデルから考えてみます。Seq2Seqモデルで翻訳を前回の記事では実装しました。Seq2Seqは素晴らしい技術ですが長い文章の翻訳が弱いという弱点があります。それはエンコーダーからデコーダーへ渡されるものがContextベクトルだけであるため、例えば翻訳の最初の部分の表現が弱くなってしまう可能性があるという問題点があったためです。Seq2Seqのモデルはわかりやすく表すと下図のような仕組みとなっていました。なおSeq2Seqに関しては前回の記事を参照ください
Attentionはこうした問題に対応するべく産まれました[ 2 Bahdanau et al, 2015 ]。Seq2Seqで実際に、どのようなことをAttentionを実現しているかと言えば、雑に言うと、seq2seqのエンコードの部分で利用したHiddenベクトルを、まとめてデコーダー部分にわたしている、というのが特徴になります。上のSeq2Seqのモデルと比較してみてください。
Seqence to seqence でAttentionの実現には、デコーダー内でまとめて渡されたHidden ベクトルの内どれが重要であるかを単語単位で調べていき、重み付けをしてSoftmaxし、加重平均しています。詳細な流れですが長くなるので説明しません。というのも、その方法よりもTransformerの方が精度があがっているため、いまさらSeq2SeqのAttentionの実装方式にフォーカスするよりは、Transformerを学んだほうが有用であるためです。(なにより、Transformerの説明の記事なので)
Seq2Seq with Attentionの実現方法については、リクエストが有れば別の機会にご紹介できればと思います。なお、Seqence to sequence のAttentionの実装方法も奥が深く、Global, local attentionなどの手法も提案されています。
Self-attention層の詳細
肝のSelf attention層です。センテンスにある各単語同士の注目度を算出していきます。注目度の算出は雑に言うと内積で求めていきます。
Self-Attentionでは、Embedding+PEされたベクトル(入力ベクトルと呼ぶことにする)から、Query, Key, Valueという3つのベクトルを作成します。
この3つのベクトルを作るためには3つの行列が必要なのですが、Self-attention層ではその3つの行列を学習で作ることが目標です。入力はすべてEmbedding+PEしたベクトルxとなります。つまり、このxに、学習で作られた行列key matrix, value matrix, query matrix を掛け合わせることで、それぞれQuery, Key, Valueベクトルを作るのです。
注目度である内積値,attentionはQuery, Key, Valueのベクトルから求めます。3つのベクトルの次元数は全て同じです。
ここでいうQuery, Key, Valueとは一体なんでしょうか? Query, Key, Valueは、同じ入力ベクトルxから生成されます。Self-Attentionという技術では、自身の入力単語群同士がどこに注目度が高くなるべきか、例えば翻訳では、様々な翻訳結果を元にきちんとした結果が算出されるような(内積値が高くなるような)行列を生み出すかを集中します。やっていることのイメージはと言うと、学習では入力ベクトルをぐるんぐるん回転させたり伸ばしたりする行列を生成し、ベクトル同士での内積値が正しく反応するように学習していっているイメージとなります。
結果として、その行列と入力ベクトルから算出したq, k, vベクトルは、学習内容に対しては、特定のセンテンス内のワード同士のAttention(内積値が高い)が完成し、例えば翻訳では、未知の入力に対してもAttentionを正確に算出することで、正確な翻訳の手助けをすることができる、という算段です。
説明が難しいのですが、Query, Key, Valueについて、何で3つに分解するんだろう、それぞれの持つ意味は何だろうかと考えすぎると思考停止に陥いってしまうので、今は取り敢えず深く考えずに3つに分解する、それを以ってなんとかSelf-attentionを実現する、という考えで読み勧めてください。
それでは、実際にどのようにSelf-attentionが実装しているのか見てみます。
Step 1:次元圧縮
今ここで, You love me( お前は俺を愛してる)の3ワードのセンテンスを例としましょう。オリジナルの論文では512次元のベクトルでしたが、今は説明のため、各ワードは16次元でembedding+PE されているとします。
まずは、16次元のワードを3次元のベクトルに落とし込みます。(3ワードの”3”とは無関係です。短縮次元はいくつでもいいのです。)。それぞれの生成行列を定義します。初期値はランダムです。
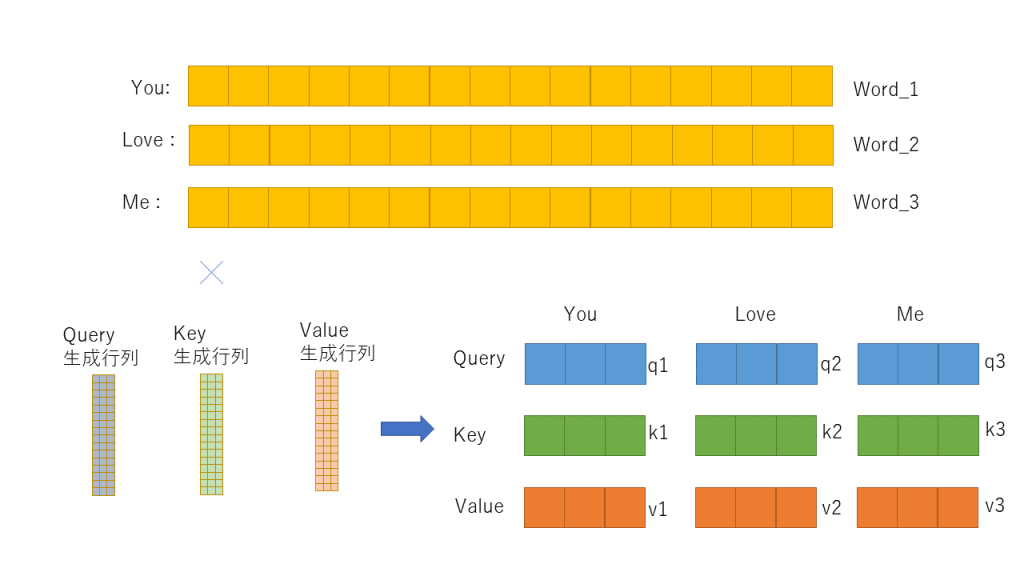
Step:2計算
上記処理を行ったあとは、ワードに対するそれぞれのquery, key, valueベクトルを用いて内積値の計算を実施します。まず、Youを例に取り、You, love, meのKeyベクトルとValueベクトルを使って結果zを取り出します。計算処理の内容については下記のとおりです。
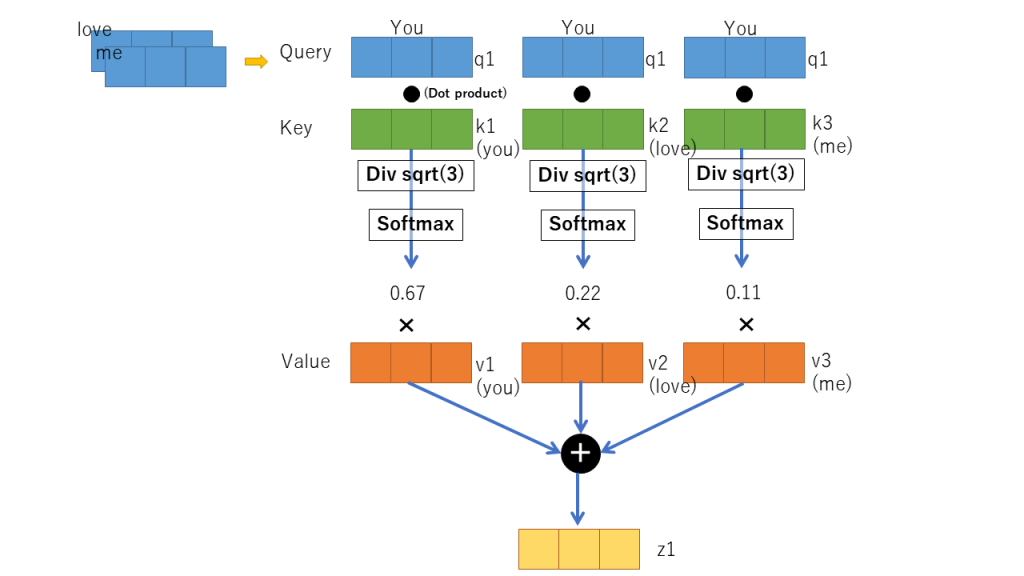
これが、Self-attention層で行われている処理です。ただし、Transformerでは上記を複数のヘッドで実装することで高速化と精細化に成功しました。Multi-head attentionと言われる実装です。
Multi-head attentionの流れ
先程説明した処理を、複数のヘッドで行うのがMulti-head attentionという処理になります。先程の説明はsingle-head と呼べるかもしれません。今回は、8つのヘッドがあるとして説明していきます。
embedding+PE された次元数が512次元だとして、まず入力を8つのヘッドで分割するものとします。すると、一つの次元は64次元となります。分割の仕方は、前からぶつ切りに切りです。
split( [ ……. ] )=> [ ….], [ ….] ,[ ….] ,[ ….] ,[ ….] ,[ ….] ,[ ….] ,[ ….]
あとは、この64次元ごとに、上記のSelf-attentionで説明したStep2の処理を行います。Multi-head attentionを行う際には Step1の次元縮小処理は必要ありません。ただ、入力値ベクトルからkey, value, query ベクトル生成用の行列は作成する必要があるので、次元を縮小せずに同じ次元で出力するような処理は必要があります。つまり、pytrochで表せば、nn.Linear( 64, 64 ) のように同じ次元を指定しています 。
さて、Multi-head attentionで処理をした結果としてですが、最終的に8つのHeadから、8つの64次元の結果が出てきます。この結果を元の分けたとおりの順番で連結し元に戻してやります。(今回の例であれば512次元にもどす)
concat( [ ….], [ ….] ,[ ….] ,[ ….] ,[ ….] ,[ ….] ,[ ….] ,[ ….] )=> [ ……. ]
これだけです。Multihead-Attentionをやる理由は、並列に処理ができるようになるため高速化が期待できることもそうですが、結果として分割して処理をすると精度が上昇するという理由もあります。そのため、実装ではMulti-head Attentionを実装します。さて、今説明した内容をソースコードで示します。
class MultiHeadSelfAttention( nn.Module ):
def __init__( self, dimention, num_head, dropout = 0.1):
super().__init__()
assert dimention % num_head == 0
self.dim = dimention
self.num_head = num_head
self.head_dim = self.dim // self.num_head
self.q_linear = nn.Linear( self.dim, self.dim )
self.k_linear = nn.Linear(self.dim,self.dim )
self.v_linear = nn.Linear(self.dim,self.dim )
self.out = nn.Linear(self.dim,self.dim )
self.dropout = nn.Dropout( dropout )
self.scale = torch.sqrt(torch.FloatTensor([self.head_dim]) )
# q = [batch size, query len, hid dim]
# k = [batch size, key len, hid dim]
# v = [batch size, value len, hid dim]
def foward( self, q, k, v, mask =None ):
batch_size = q.size( 0 )
Q = self.q_linear(q) # [batch size, query len, dimention]
K = self.k_linear(k)
V = self.v_linear(v)
Q = Q.view(batch_size, -1, self.num_head, self.head_dim).permute(0, 2, 1, 3) # [batch size, n heads, query len, head dim]
K = K.view(batch_size, -1, self.num_head, self.head_dim).permute(0, 2, 1, 3)
V = V.view(batch_size, -1, self.num_head, self.head_dim).permute(0, 2, 1, 3)
self.k_linear( k ).view( batch_size, -1, self.num_head, self.head_dim)
energy = torch.matmul(Q, K.permute(0, 1, 3, 2)) / self.scale # [batch size, n heads, query len, key len]
if mask is not None:
energy = energy.masked_fill(mask == 0, -1e10)
attention = torch.softmax( energy, dim = -1 ) # [batch size, n heads, query len, key len]
x = torch.matmul(self.dropout(attention), V) # [batch size, n heads, query len, head dim]
x = x.permute(0, 2, 1, 3).contiguous().view(batch_size, -1, self.dim) # [batch size, query len, dim]
return self.out( x ), attention # self.out(x) == [batch size, query len, hid dim]
4.ノーマライゼーション層(+ residual の説明 )
標準化、正規化、規格化など、呼ばれるノーマライゼーションにより安定した学習が出来るようになります。中で実装している内容ですが、値を平均から引き、標準偏差で割るような操作をしてやります。平均が0で、分散が1になります。まさにノーマライゼーションですね。
言葉だとわかりにくいので、どういう処理をしているのか、ある人[6]がソースコードを書いていました。参考にしてみてください
class Norm(nn.Module):
def __init__(self, dimention, eps = 1e-6):
super().__init__()
self.size = dimention
self.alpha = nn.Parameter(torch.ones(self.size))
self.bias = nn.Parameter(torch.zeros(self.size))
self.eps = eps
def forward(self, x):
norm = self.alpha * (x - x.mean(dim=-1, keepdim=True)) / (x.std(dim=-1, keepdim=True) + self.eps) + self.bias
return norm
residual(残差処理) の説明
残差処理といいますが、Encoderを構築する際に、Multi header attention で出てきた出力値に、元々の入力Inputを足し合わせます。そしてNormalization処理をします。疑似コードであらわすと、単に次のような操作をしているだけです。
y = Normlization( MulitHeadderAttention( input ) + input )
これを残差処理といいます。下記のオリジナルの論文を見ると、Add&Norm内で入力値を持ち込んでいるので残差処理をしているのがわかります。
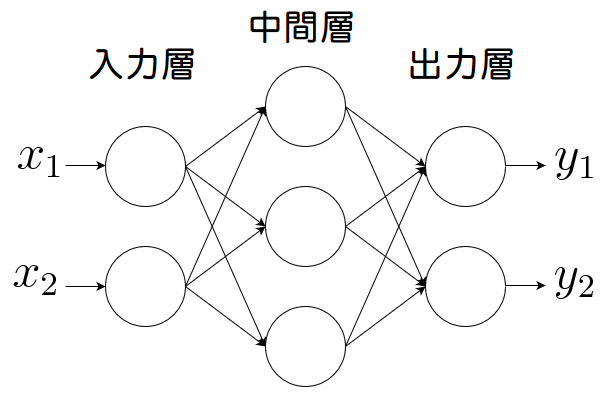
5.Feed Forward 層
Feed Fowardでは、2層の全結合層からなるニューラルネットワークを実装しています。また、Dropoutも定義することで過学習を抑制します。Dropoutに関しては、次の記事が明るいです。[14]
数式ではつぎのようなことを行っています。
FFN(x)=max(0,xW1+b1)W2+b2
図では次のとおりです。いえば、ただのニューラルネットワークです。
ソースコードで実際に表現すると、次のような単純な処理をしているだけです。
class FeedForward(nn.Module):
def __init__(self, dimention, d_ff=2048, dropout = 0.1):
super().__init__()
self.linear_1 = nn.Linear(dimention, d_ff)
self.dropout = nn.Dropout(dropout)
self.linear_2 = nn.Linear(d_ff, dimention)
def forward(self, x):
x = self.dropout(F.relu(self.linear_1(x)))
x = self.linear_2(x)
return x
ここまでで、Encoderで使われている全てのパーツの説明がおわりました!実はEncoderもDecoderもほとんど同じパーツを使います。唯一,Encoder-decoder attention層だけがちがうのですが、その解説を行います。
Decoder: Encoder-DecoderAttention層
改めてTransformerの全体図をみてみると、次のようになっています。
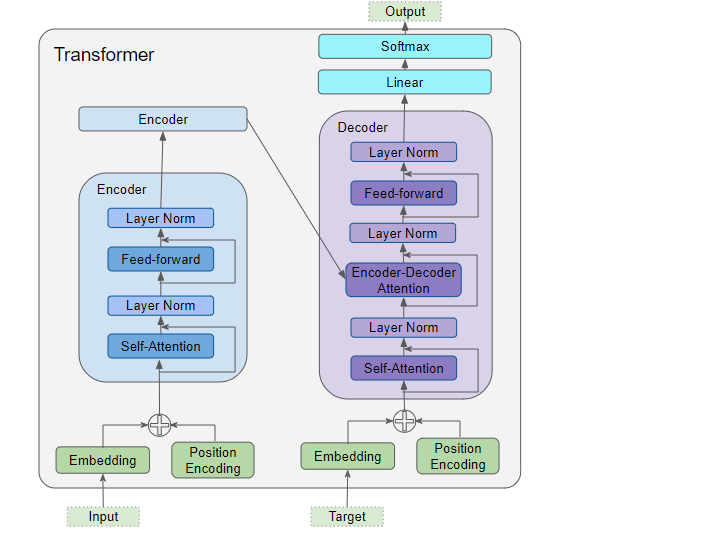
ブロックを見てみると殆どの解説が終わっている部分ばかりです。唯一Encoder-DecoderAttentionだけ説明をしていませんでした。ただ、Encoder-Decoder Attentionは次の画像がとてもわかり易いかと思います。
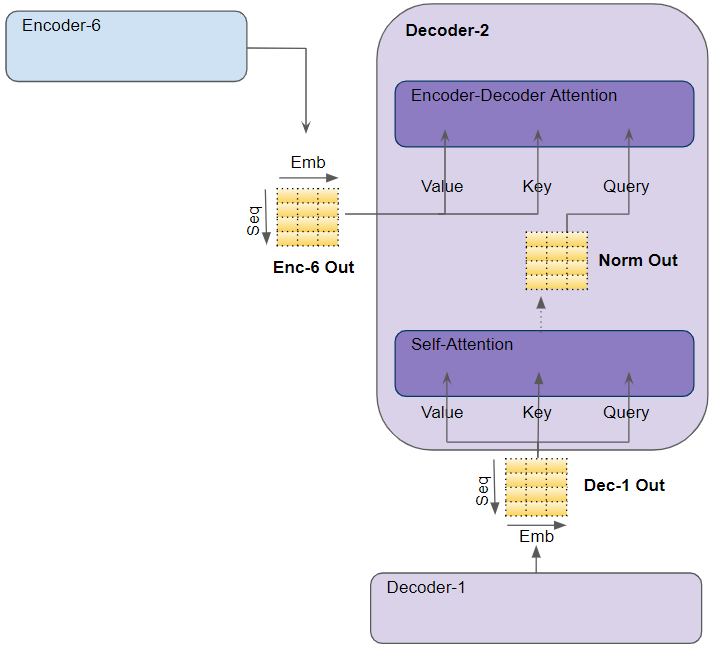
やっていることはSelf-attentionと一緒です。ただし、Encoder-Decoder層では、最後のEoncoderパートで出力された値を、Value, Keyベクトルを生成するための入力として渡します。Queryベクトルを作成するための入力に関しては、Decoder内部のself attentionでの出力値を使います。
内部で計算する処理は、Self-attention層の計算した方法(Multi-attentionで説明した計算方法)と全く同じロジックで計算するのです。これだけとなります。
なお、入力に対してまだ出現していないもので推測するのはおかしいというロジックの元、マスクをかけることがあります。
Transformer 全体像とEncoder, Decoderの実装
改めてTransformer全体像
さて、いままで説明してきたものを連結していくとTransformerの完成です。改めて全体像の画像を見てみます。

上記の図でNxと書いてあることに気づきますが、これは複数個、縦につなげるということを意味しています。オリジナルの論文だと6段の構成となっています。
Encoderの実装
N段構成を担う、一つのEncoderブロックの実装例を以下に示します。
class EncoderBlock(nn.Module):
def __init__(self, dimention, n_heads, dropout ):
super().__init__()
self.self_attention = MultiHeadSelfAttention( dimention, n_heads, dropout )
self.self_attn_layer_norm = nn.LayerNorm(dimention)
self.ff_layer_norm = nn.LayerNorm(dimention)
self.feadforward = FeedForward(dimention)
self.dropout_1 = nn.Dropout(dropout)
self.dropout_2 = nn.Dropout(dropout)
def forward( self, x, src_mask ):
#x = [batch size, src len, dim]
#src_mask = [batch size, 1, 1, src len]
new_x, _ = self.self_attention( x, x, x, src_mask)
new_x = self.self_attn_layer_norm(x + self.dropout_1(new_x)) #src_x = [batch size, src len, dim]
out_x = self.feadforward(new_x)
out_x = self.ff_layer_norm(x + self.dropout_2(out_x)) #out_x = [batch size, src len, dim]
return out_x
さて、ブロックができればいよいよエンコーダーです。
class Encoder(nn.Module):
def __init__(self, vocab_size, dimention, Nx, n_heads, dropout = 0.1, max_word_len = 100):
super().__init__()
self.embed = nn.Embedding(vocab_size, dimention)
self.pe = PositionalEncoder( max_word_len, dimention)
self.blocks = nn.ModuleList([ EncoderBlock( dimention, n_heads, dropout ) for _ in range(Nx) ] )
self.norm = Norm(dimention)
#src = [batch size, src len]
#src_mask = [batch size, 1, 1, src len]
def forward(self, src, src_mask):
x = self.embed(src)
x = self.pe(x)
for encoder_block in self.blocks:
x =encoder_block(x, src_mask) #src = [batch size, src len, hid dim]
return self.norm(x)
Encoder内のNxは何段のブロックを使うか、n_headsはmulti-head attentionのヘッダーのサイズを表しています。
Decoderの実装
続いて、デコーダーです。まずはDecoderを構成する1つのブロックのソースコードを記載します。
class DecoderBlock(nn.Module):
def __init__(self, dimention, n_heads, dropout ):
super().__init__()
self.norm1 = nn.LayerNorm(dimention)
self.norm2 = nn.LayerNorm(dimention)
self.norm3 = nn.LayerNorm(dimention)
self.dropout = nn.Dropout(dropout)
self.attention_self = MultiHeadSelfAttention(dimention, n_heads, dropout)
self.attention_encoder = MultiHeadSelfAttention(dimention, n_heads, dropout)
self.feedforward =FeedForward(dimention)
#x = [batch size, target len, hid dim]
#enc_src = [batch size, src len, hid dim]
#target_mask = [batch size, 1, target len, target len]
#src_mask = [batch size, 1, 1, src len]
def forward(self, x, x_from_encoder, target_mask, src_mask):
_target, _ = self.attention_self(x, x, x, target_mask)
x = self.norm1(x + self.dropout(_target)) #x = [batch size, target len, hid dim]
_target, attention = self.attention_encoder(x, x_from_encoder, x_from_encoder, src_mask)
x = self.norm2(x + self.dropout(_target)) # target = [batch size, target len, hid dim]
_target = self.feedforward(x)
x = self.norm3(x + self.dropout(_target)) # target = [batch size, target len, hid dim],
return x, attention # attention = [ batch size, n heads, target len, src len ]
上記のデコーダーブロックを使いデコーダーを実装します。
class Decoder(nn.Module):
def __init__(self, vocab_size, dimention, n_layers, n_heads, dropout = 0.1, max_word_len = 100):
super().__init__()
self.embed_vocab = nn.Embedding( vocab_size, dimention ) #
self.pe = PositionalEncoder( max_word_len, dimention)
self.blocks = nn.ModuleList( [ DecoderBlock(dimention, n_heads , dropout ) for _ in range(n_layers) ] )
self.scale = torch.sqrt(torch.FloatTensor([dimention]))
self.norm = Norm(dimention)
#trg = [batch size, trg len]
#enc_src = [batch size, src len, dimention]
#trg_mask = [batch size, 1, trg len, target len]
#src_mask = [batch size, 1, 1, src len]
def forward(self, target, x_from_encoder, trg_mask, src_mask):
x = self.embed_vocab( target )
x = self.pe( x )
for decoder_block in self.blocks:
x, attention = decoder_block(x, x_from_encoder, trg_mask, src_mask) #target = [batch size, trg len, hid dim], attention = [batch size, n heads, trg len, src len]
output = self.norm(x) #output = [batch size, trg len, output dim]
return output , attention
ほとんどEncoderと変わらないような構成をしています。
Transformerの実装
いよいよTransformerの実装です。すでにEncoder, Decoderは実装しているので、これを利用するだけです。
class Transformer(nn.Module):
def __init__(self, src_vocab, trg_vocab, d_model, N, heads):
super().__init__()
self.encoder = Encoder(src_vocab, d_model, N, heads )
self.decoder = Decoder(trg_vocab, d_model, N, heads )
self.out = nn.Linear(d_model, trg_vocab)
def forward(self, src, target, src_mask, trg_mask):
output_encoder = self.encoder(src, src_mask)
output_decoder = self.decoder(target, output_encoder, trg_mask, src_mask )
output = self.out(output_decoder)
return output
終わりに
今回はTransformerについてアルゴリズムをソースコード付きで解説しました。意外と単純な構成をしているんだと気づいたと思います。いまはやりのGPT-3,BERTなどの最先端の学習は、すべてTransformerの技術が基本になっています。まずは今回の記事でTransformerとはどういったものか感じていただけると幸いです。
参考文献
[3] https://ai.googleblog.com/2017/08/transformer-novel-neural-network.html
[4] https://jalammar.github.io/illustrated-transformer/
[5] https://mchromiak.github.io/articles/2017/Sep/12/Transformer-Attention-is-all-you-need/#.XIWlzBNKjOR
[6]https://towardsdatascience.com/how-to-code-the-transformer-in-pytorch-24db27c8f9ec
[9]https://towardsdatascience.com/how-to-code-the-transformer-in-pytorch-24db27c8f9ec
[10]https://pytorch.org/tutorials/beginner/nlp/word_embeddings_tutorial.html
[11]https://kazemnejad.com/blog/transformer_architecture_positional_encoding/
[12]https://medium.com/swlh/elegant-intuitions-behind-positional-encodings-dc48b4a4a5d1
[13]https://data-science-blog.com/blog/2021/04/07/multi-head-attention-mechanism/
[14]https://medium.com/axinc/dropout%E3%81%AB%E3%82%88%E3%82%8B%E9%81%8E%E5%AD%A6%E7%BF%92%E3%81%AE%E6%8A%91%E5%88%B6-be5b9bba7e89
[15] https://pytorch.org/docs/stable/generated/torch.nn.LayerNorm.html
[16]https://kikaben.com/transformers-encoder-decoder/
[17]https://medium.com/@smitasasindran/12-attention-mechanisms-multihead-attention-958041a35553