近年、ディープラーニング業界、はたまた画像処理業界ではGANとVAEの2つの技術で話題が持ちきりとなりました。GANについては前回解説しました。今回はそんなVAEのアルゴリズムについて解説をしていきます。GAN同様に最後にPyTorchによる実装例を紹介していきます。
VAEとは
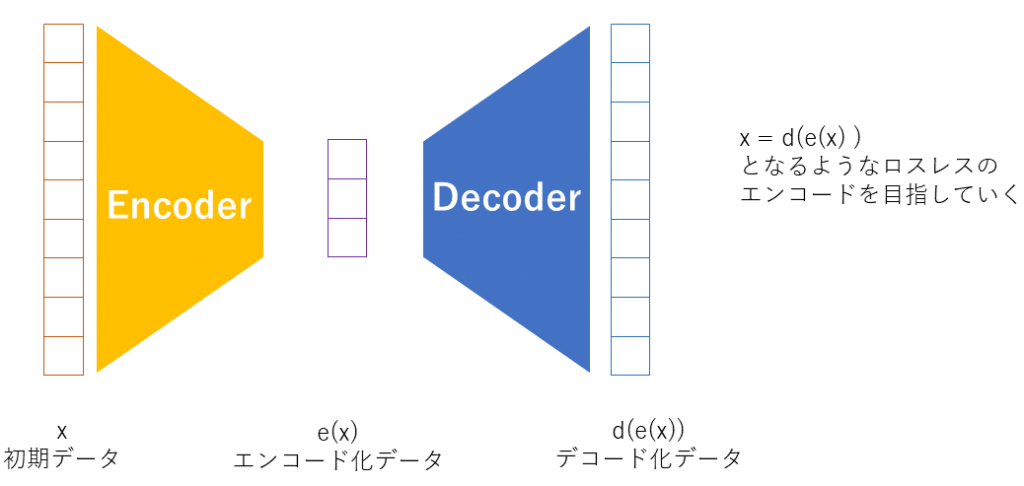
VAEは情報を圧縮して圧縮した情報から元の情報に戻す、というような仕組みをもった、AE(Auto encoder)と言われるものの一種です。AEはただ単にデータの圧縮と再構築をするだけでしたが、VAEは確率モデルの理論を導入しています。VAEは確率分布を使ったモデルということは、未知のデータを確率的に作成できることになります。VAEはGenerative model(生成モデル)と言われています。トレーニングデータからProbability Density Function (PDF)を推定するモデルであるためす。
GANと違って何ができるのか
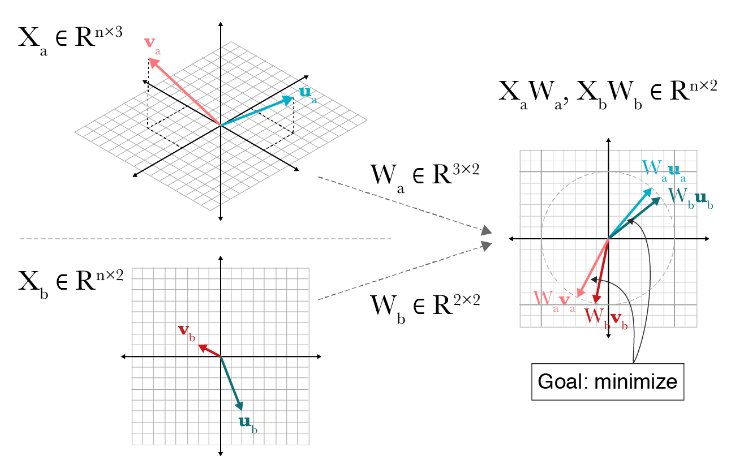
VAEの一つの特徴は次元削減です。次元削減といえばPCAやSVDなどを思い浮かべるかもしれません。VAEは同様にLatent space(潜在空間)に次元圧縮し、またそこから復元するということをしています。
PCAのように圧縮した次元において直行している必要はありません。この辺も普通の次元圧縮とのアプローチとは異なっています。
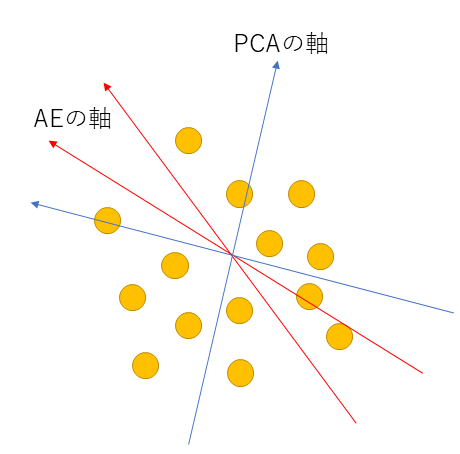
AEとVAEは違いがあまり無く感じますが、前述の通り確率を用いたところに違いがあります。AEは点(Single point)としてデータを潜在空間にマッピングしていましたが、VAEでは潜在空間に落とし込むときにガウス分布に従って落とし込ませます。デコーダーはその点を拾ってデコードするため、見方を変えれば、確率的にサンプリングしてzを拾っている、ということになるのです。このzをデコードして元の入力に近づけるようにするのです。
さて、VAEは確率モデリングと言われます。確率モデリングとは、例えば何かのデータxが分布していたとして、その分布を確率で表現するというモデルです。あるデータxが正規分布に従っていたとしたら、データxの確率分布は正規分布となり、P(X)=正規分布( μ, σ )と言う感じで表現します。P(X)と書くと思わずPは関数と勘違いするかもしれませんが、確率を表すものなので注意が必要です。
画像処理でVAEの例
VAEを画像処理に適用した場合は連続画像を取り扱うことができる、というのは聞いたことがあると思います。それはなぜかというと、エンコードした空間e(X)が確率を用いた分布で表されているためです。
パラパラマンガを想像してみてください。あるフレームと、その次のフレームがある時、2枚のフレーム同士はエンコードした空間において、近いところにあるはずです。(近いところにあるようにするのがVAEの目的であるためです)。この2枚のフレームの中間の画像は、エンコードした空間においてどこにあるのでしょうか?それは同じ空間内のちょうど中間のところにある確率が高いと推測できます。つまりそこの情報をデコードすれば、中間画像が生成されそうです。VAEではこうした事ができるため、連続画像に強いと言われています。
数式
VAEはデータを確率モデル化をすることを目標とします。データをX、その確率分布をP(X)と定義すれば、P(X)を見つけること、すなわちP(X)の最大化がVAEの目的です。そしてP(X)に関しては次のように表現することができます。[1]
P(X) = \int P(X \vert z) P(z) dz = \int P(X,z)上記の式はXが入力画像と考え、その画像を表現する潜在ベクトルzを少なくとも1つ見つけたいという意味があります。
また、事前分布P(z)から\{z_i\}_{i=1}^nをサンプルした際に、P(X)を次のように近似できます。
P(X) \approx \frac{1}{n}\sum_{i=1}^n P(x|z_i)P(X)を求めればいいのですが、一筋縄には行きません。それはXが高次元であることもそうですが、その確率を求めるのにはすべてのzの空間を舐め回すような非常にたくさんのサンプリングが必要なだけでなく、組み合わせをチェックするような処理が必要となり、総当りでP(X)を求めることは現実的ではありません。
そのため、P(X)を求めるには別のアプローチを考えます。もし事後確率のP(z|X)がもとめられれば、p(x|X)=\int P(x|z)p(z|X) dz より未知の画像xを作り出すような確率分布を求めることができそうです。そうなると 事後確率のP(z|X)を求めるだけとなり、簡単に思えますが事後確率はベイズの定理により次の式になります。
P(z|X) = P(X|z)\cfrac{P(z)}{ P(X)}よく見るとあの厄介なP(X)が分母にあります。やはり求めることができません。
ここで、諦めずに別のアプローチで P(z|X) を求めていくようにしていきます。
P(z|X) を求める
P(z|X)を求めるにあたり少し工夫します。ここでVAEの名前の由来ともなっていますが、 Variational Inference(VI) という手法を使います。P(z|X)を推定するためにQ(z|X)という分布を考えます。Q(z|X)はP(z|X)の近似で、ガウス分布などの簡単な分布関数の組み合わせによりP(z|X)を近似します。
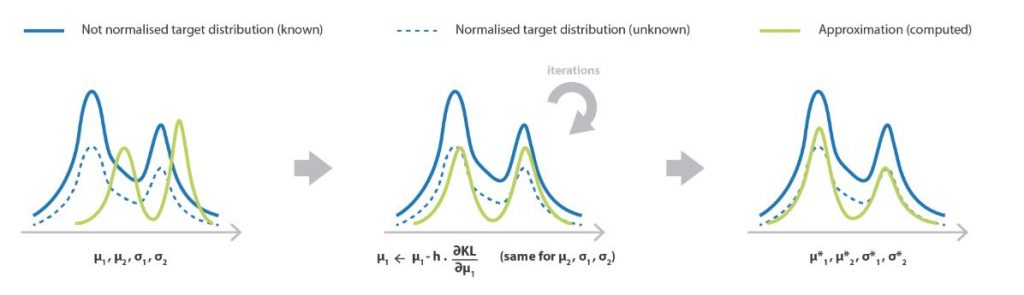
どれだけ似ているのか、という指標については類似尺度としてKLダイバージェンスを使います。同じ分布であれば0に、異なれば値が大きくなっていくような関数です。KLダイバージェンス次のように書くことが出来ます。
KL(P||Q) = E_{x \sim P(x)} log \cfrac{P(x)}{Q(x)}=\int_{-\infty}^{\infty}P(x)\ln \cfrac{P(x)}{Q(x)}dxここから式が多く出てくるので、見やすくするために単純にP(z|X )をP, Q( z|X)をQと表示します。Qの近似は次のようにかくことができます。
\begin{aligned} D_{KL}[Q\Vert P] &= \sum_z Q \log (\cfrac{Q}{P}) \\ &=E [ \log (\cfrac{Q}{P}) ] \\ &= E[\log Q - \log P] \end{aligned}最後はlogの変換公式により、割り算を引き算にしただけです。さてP である P(z|X ) は P(z|X) = P(X|z)P(z) / P(X) のように表現できたので、先の式に当てはめてみましょう。
\begin{aligned} D_{KL}[Q\Vert P] &= E[\log Q - (\log (P(X \vert z) \cfrac{P(z)}{P(X)})] \\ &= E[\log Q- \log P(X \vert z) - \log P(z) + \log P(X)] \end{aligned}ここでzに関する期待値でくくっている項に注目するとP(X)があります。P(X)はzに関係ありません。そのため括弧の外に出すことができます。
\begin{aligned} D_{KL}[Q\Vert P] &= E[\log Q- \log P(X \vert z) - \log P(z)] + \log P(X) \\ D_{KL}[Q\Vert P] - \log P(X) &= E[\log Q- \log P(X \vert z) - \log P(z)] \end{aligned}ここからがトリッキーなのですが、右辺に注目するともう一つのKLダイバージェンスを見つけることができます。先の式を両辺にマイナス倍します。
\begin{aligned} \log P(X) - D_{KL}[Q\Vert P] &= E[-\log Q + \log P(X \vert z) + \log P(z)] \\ &= E[\log P(X \vert z) -( \log Q - \log P(z))] \\ &= E[\log P(X \vert z)] -E[( \log Q - \log P(z))] \\ &= E[\log P(X \vert z)]- D_{KL}[Q\Vert P(z) ] \end{aligned}なんとPとQを近づけようとした結果、本来の目的であったP(X)に関する式がでてきてしまいました。PとQを縮約して記載していたので、正しく展開してかいてみます。
\log P(X) - D_{KL}[Q(z \vert X) \Vert P(z \vert X)] = E[\log P(X \vert z)] - D_{KL}[Q(z \vert X) \Vert P(z)]本当の目的はP(X)の最大化でした。結局ですが、これを最終的なVAEの目的の関数として定義することになります。
最終的に得た式は非常に興味深い構造になっています。
- Q(z|X) はデータXを受取り、潜在空間にzを投影
- zは潜在変数
- P(X|z)は潜在変数zからデータ生成
つまりQ(z|X)はエンコーダ、zは潜在変数(エンコードされたデータ),そしてP(X|z)はデコーダです。まさにオートエンコーダーそのものとなりました。
算出された式を観察して、左辺と右辺がありますが、左辺にあるlog(p)最大化することが目的でした。そのためには右辺を最大化していくこと、つまり E[\log P(X \vert z)] を大きくして D_{KL}[Q(z \vert X) \Vert P(z)]を小さくしていくことで、左辺は大きくなっていきます。
そのため、今度は目的を右辺の最大化に絞っていきます。
右辺を最大化する。
右辺には以下の2つの式があります。
- E[\log P(X \vert z)]
- D_{KL}[Q(z \vert X) \Vert P(z)]
右辺=数式1-数式2、ですので数式1を最大化、数式2は最小化していけば、右辺は大きくなり目的が達成されます。
まず 数式 1についてですが、よく見ると潜在変数zを受取りXを生成する教師つきの学習そのものです。ですので、学習によりなんとかなりそうです。
さて、厄介なのが 数式 2です。ここで一つの仮定を起きます。P(z)は正規分布N(0, 1)と仮定するのです。そして、Xからzを生成する分布もパラメータ\mu(X), \sigma(X)付きの正規分布となります。 平均と分散はXを中心としたという意味です。そして、KLダイバージェンスは次のように表されます。
D_{KL}[N(\mu(X), \Sigma(X)) \Vert N(0, 1)] = \frac{1}{2} \, \left( \textrm{tr}(\Sigma(X)) + \mu(X)^T\mu(X) - k - \log \, \det(\Sigma(X)) \right)kはガウシアンの次元数、traceは対角要素の和を表します。そして、detは対角要素の積\det \left({\mathbf A}\right) = \prod_{i \mathop = 1}^n a_{ii}です。
導出に関しては、ここでは重要でないため割愛しますが最終的には次のようになります。(導出に関して興味ある方は[2]を参照してください。)
D_{KL}[N(\mu(X), \Sigma(X)) \Vert N(0, 1)] = \frac{1}{2} \sum_k \left( \exp(\Sigma(X)) + \mu^2(X) - 1 - \Sigma(X) \right)この項目を実装するときにはロス関数の中で利用します。実際との差分を計算するためですね。
全ての要素の説明ができました。あとはやるだけです。
実装
エンコーダーとデコーダーの実装は次のとおりです。
エンコーダー
class Encoder( nn.Module ):
def __init__( self ):
super().__init__()
self.common = nn.Sequential(
nn.Linear( 784, 400 ),
nn.ReLU(),
)
self.model1 = nn.Sequential(
self.common,
nn.Linear( 400, 20 )
)
self.model2 = nn.Sequential(
self.common,
nn.Linear( 400, 20 )
)
def forward( self, img ):
img_flat = img.view( img.size( 0 ), -1 )
return self.model1( img_flat ), self.model2( img_flat )
デコーダー
class Decoder( nn.Module ):
def __init__( self ):
super().__init__()
self.model = nn.Sequential(
nn.Linear( 20, 400 ),
nn.ReLU(),
nn.Linear( 400, 784 ),
nn.Sigmoid(),
)
def forward( self, z ):
return self.model( z )
エンコーダーとデコーダーを用いいたVAEを次のように実装していきます。
VAE
class VAE( nn.Module ):
def __init__( self ):
super().__init__()
self.encoder = Encoder()
self.decoder = Decoder()
def _reparameterization_trick( self, mu, logvar ):
std = torch.exp( 0.5 * logvar )
eps = torch.randn_like( std )
return mu + eps * std
def forward( self, _input ):
mu, sigma = self.encoder( _input )
z = self._reparameterization_trick( mu, sigma )
return self.decoder( z ), mu, sigma
説明ではzの取得は正規分布でのサンプリングを仮定しました。ところが実際にサンプリングするとバックプロパゲーションが出来ないため学習が出来ません。そこでreparameterization trickというのを用いいます。zを次の式で近似します。
z = \mu(X) + \Sigma^{\frac{1}{2}}(X) \, \epsilon where, \epsilon \sim N(0, 1)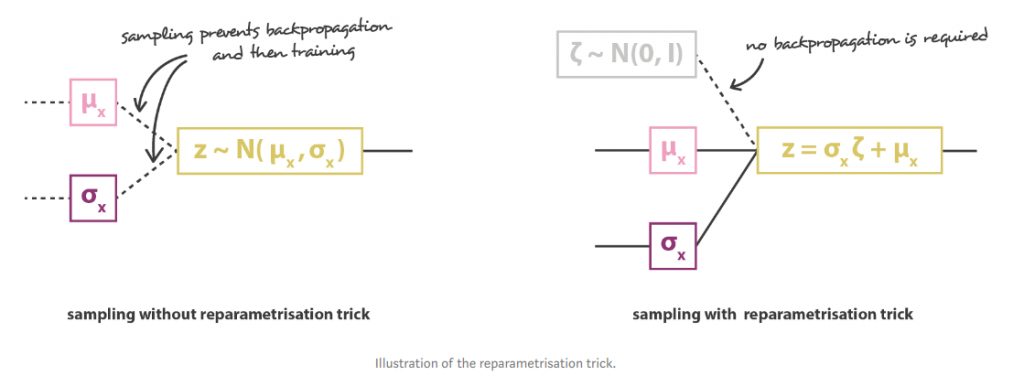
最後に損失関数とVAEを使ったコードは次のとおりです。
# Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
# 入力画像をどのくらい正確に復元できたか?
def VAE_LOSS( recon_x, x, mu, logvar ):
# 数式では対数尤度の最大化だが交差エントロピーlossの最小化と等価
BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), size_average=False)
# 潜在空間zに対する正則化項. # P(z|x) が N(0, I)に近くなる(KL-distanceが小さくなる)ようにする
KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
return BCE + KLD
def main():
epoch_size = 50
vae = VAE()
vae.cuda()
Tensor = torch.cuda.FloatTensor
dataloader=get_dataloader()
optimizer = torch.optim.Adam( vae.parameters(), lr=1e-3 )
for epoch in range( epoch_size ):
for i, ( imgs, _ ) in enumerate(dataloader):
optimizer.zero_grad()
real_images = Variable( imgs.type( Tensor ) )
gen_imgs, mu, logvar = vae( real_images )
loss = VAE_LOSS( gen_imgs, real_images, mu, logvar ).cuda()
loss.backward()
optimizer.step()
VAE_LOSSでは得た画像が目的とした式と同じになるような差分を計算しています。
長くなりましたがこれがVAEの全貌です。今回のソースコードはGithubにあげてあります。
https://github.com/octopt/techblog/blob/master/vae/main.py
参考文献
- https://en.wikipedia.org/wiki/Law_of_total_probability
- https://wiseodd.github.io/techblog/2016/12/10/variational-autoencoder/
- https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73