正準相関分析(Canonical Correlation Analysis：CCA)

はじめに

１つの目的変数を、複数の変数から説明するのが重回帰分析でした。正準相関分析は、複数の目的変数に対して、複数の変数がどう説明するのか見る方法です。

重回帰分析の際には、1つの変数を説明するために複数の変数を使っていましたが、正準相関分析は複数の変数を説明するために複数の変数を使います。重回帰分析の一般化、としてみることが出来ます。

数学的な意味の正準相関分析

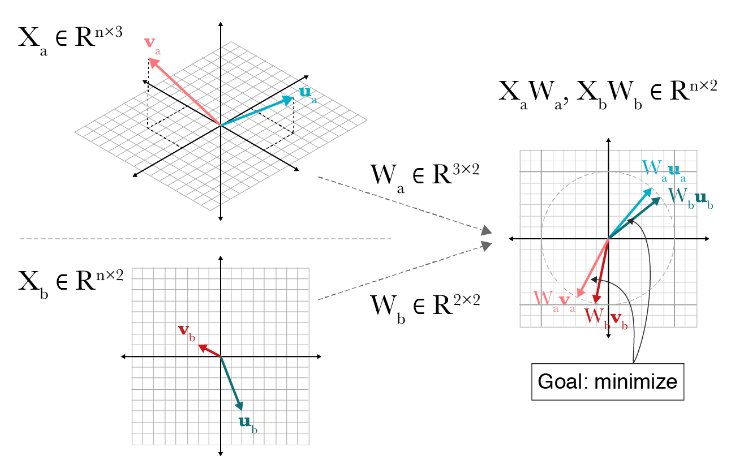
数学正準相関分析は、「複数の変数を2つの合成変数にまとめ、その合成変数間の相関係数を最大にする」という手法です。

つまり数に重み係数をつけて足し合わせたものを変量（正準変量、合成変量とも呼ばれる）として、その変量同士の相関関係である正準相関係数を最大にするような重み相関係数を求めます。

変量は回帰分析においてのy=axにおいてのyの部分です。回帰分析の場合、yの値が決まっていますが、正準相関分析ではyの値は決まっておらず、解析結果によって求めます。

正準相関分析は共通の空間(正準空間)に写像する手法です。

複数の情報源に共通して含まれる情報だけを抽出することによって、情報を統合するための次元圧縮法とも考えることが出来ます。

正準相関分析の具体例

理論だと少しむずかしいので具体的な例で説明します。「数学点数、日本史点数、握力、遠投距離 」 のデータが5人分あったとします。

people1=[90, 40, 50,30]
people2=[80, 50, 55,10]
people3=[30, 80, 40,5 ]
people4=[50, 50, 35,50]
people5=[70, 80, 30,40]

同じ人たちの「走り幅跳び距離、英語点数」のデータもあります。

people1=[1.5, 40]
people2=[3.1, 30]
people3=[1.7, 50]
people4=[0.5, 80]
people5=[1.3, 90]

走り幅跳び距離と英語点数が、どう影響を受けるかということを考えることができます。

２つグループの相関関係を無理矢理最大化するような式をそれぞれ作ってやる、という事が正準相関分析となります。先に説明したとおり、解析結果後にそれぞれのグループで合成変量がでてきます。y=aXでいうところのyの部分です。このyの値をどう捉えるかはその観測者次第となります。

分析結果については、PCAのように寄与率と、最も相関があるように出来た重みが出てきます。N次元のデータであれば、N個の軸での解析が可能です。ただ、２つのグループの次元が違う場合がほとんどです。その場合は、最も長い次元にあわされますが、経験的に５−６個の軸から見れば大体解析できます。以下にCCAのコードを記載します。（察しの通り、正方行列ではないので特異値分解を中でおこなっています）

from sklearn.cross_decomposition import CCA
    cca = CCA(n_components=5)
    cca.fit(X1, X2) 

n_componentsは、寄与率の高い上から何個までの重み群と寄与率取ってくるのか、指定するものです。解析した異次元数を表しています。

CCAが中で何をしているかは、数学的な説明が多くなる為詳細を省きます。正準相関分析に関して解き方などの理論が気になる方は、君山 由良先生の多変量回帰分析・正準相関分析・多変量分散分析―多変量間の相関と因果関係の因子 (統計解説書シリーズ A-16) をおすすめします。非常に丁寧に解説されております。

参考文献

• 多変量回帰分析・正準相関分析・多変量分散分析―多変量間の相関と因果関係の因子 (統計解説書シリーズ A-16)
• https://gregorygundersen.com/blog/2018/07/17/cca/

おすすめサイト

• 回帰分析(重回帰分析）
• 最小二乗法による重回帰分析
• Variational AutoEncoder( VAE )
• ロジスティック回帰分析
• 最尤法
• 単純ベイズ分類器(Naive Bayes Classifier )
• 数量化理論Ⅳ類(MDS)
• 線形判別分析(LDA)
• 主成分分析(PCA)
• 特異値分解(SVD)