FPマイニング(頻出パターンマイニング )

FPマイニングとはFrequency Pattern Mining の略で、物事の関連を見出すことを目的とします。たとえば、「おむつを買った人とはビールを買う」などそうした関連を見出すことを目的とします。どういうところで活躍しているのでしょうか？たとえば広告の技術などで活躍します。例えば、AというサイトをみてBというサイトを見たい人はCという商品が欲しい。それではCの広告を出そう！という事になります。こうした関連性を見出したいときはFPマイニングが利用されます。それでは説明に入っていきます。

アソシエーションルール

「アソシエーションルール」という言葉は、日本語で、連関ルール、関連ルール、相関ルール（⇐ 全部同じ意味を表す）と呼ばれています。記号で表すと以下のようになります。

{X}→{Y}

XであればYであるという意味で。よく例題で用いられるのはビールと紙おむつです。

　 ｛ビール} →{紙おむつ}

上記の意味は「ビールを買った人はおむつを買う」という意味です。

FPマイニングはそのまんま実装すれば非常に簡単ですが問題があります。データ量が多くなると、とたんに難しくなるということです。これは、全ての組み合わせを探索する必要があるため、組み合わせ爆発が発生することによります。（要素数をXとすると２Xパターンが存在）

そのため工夫としてAprioriアルゴリズムやFP-Growth といった手法がとられており、実際にはFP-Treeを構築するFPGrowthがというアルゴリズムが用いられています。

アソシエーションルールの評価方法について

アソシエーションルールの評価方法には全部で３つの指標があります。

  1. 支持度( support )
  2. 確信度( confidence )
  3. リフト( lift )

結局は確信度が大事なわけなのですが、確信度は支持度（Support, sup)で算出されるため、Supを効率的に算出することを目標としています。

まずは、上記１，２，３それぞれの式がどのように表されるか説明いたします。

1. ルールX ⇒ Y の支持度

supp（X ⇒ Y） = σ（X ∪ Y）/ M

2. ルールX ⇒ Y の確信度

conf （X ⇒ Y） = σ（X ∪ Y）/ σ（X） もしくは、

conf （X ⇒ Y） = supp（X ⇒ Y） / supp（X）

3. ルールX ⇒ Y のリフト

lift（X ⇒ Y） ＝ conf （X ⇒ Y） / supp（Y）

ここで、上記のσの意味は全体の集合から、要素Xを含むのが幾つあったのかを表すために用いられています。

例えば、集合が３つあったとして、それぞれの要素X, Y, Z, Wは次のようになっているとします。

{X, Y}, {X,Z}, {X, Y, Z, W} 

ここで、σ( X )は 3となります。そして、XとYをふくんでいる集合の数はσ( X ∪ Y ) = 2　となります。なお、集合の数は３つなので、式中にあるMは３となります。
それぞれの「支持」「確信」「リフト」に関して説明は以下のとおりです。

  • 支持度については全体の集合からそのルールが幾つあったのかという確率である。
  • 確信度については、ルールXがあったときに Yも発生する確率である。（XであればYも買う確率）
  • リフトについては 確信度を支持度で割っている。支持度がひくければ低いほど値が高く（データの中から出現度合いが低いとリフトが上がる）、確信も高いと高くなる。これは、確率P r ( X∪Y ) /Pr(X)Pr(Y)の近似値としても知られている。ちなみ、これは相関である。つまりLIFTは相関を表している。
    • Liftは同じ確信があるときに、どちらの商品が人気あがあるのかがよくわかる。例えば、0.3/0.1, 0.3 / 0.05だと後者の方が大きい。除数は支持率（全体の数である）

３つの指標において、最終的に関連が高いものは次の二つの事が言えます。

  • 確信度conf が高い
  • 支持度support が高い

FPマイニングはこうした数値を出して、確信度が高い！支持度が低かった！など分析していくことです。

前述のとおり、全探索すれば関連性は見いだせるのですが全てでるので良いのですが、実際には不可能です。そのため、以下のような簡略化するアルゴリズムが用いられます。

Support（頻度）さえでれば、Confidenceが求まることになります。Confidence( ビール →おむつ ) = support( {ビール、おむつ} ) / support( ビール )

ですので、どのように効率的にSupportをだすかが鍵となります。

Apriori アルゴリズム

全データ数を見て、その関連を見つけるのは大変です。（組み合わせ爆発問題）。そのためAprioriアルゴリズムによって効率的に上記のアソシエーションルールを満たすものを探し出します。以下はその様子を図示した内容です。

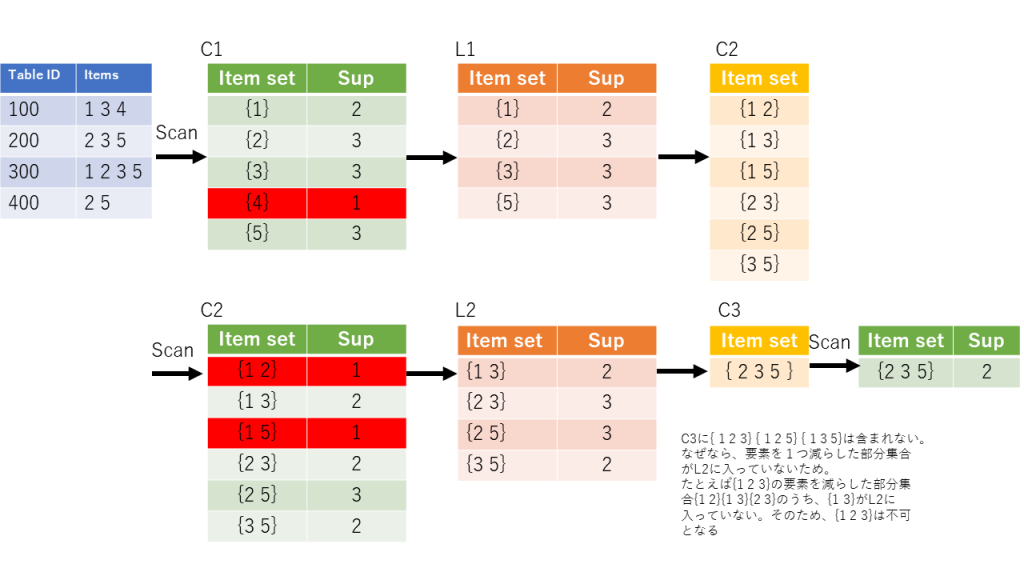
集合から、要素を取り出し、その数をカウントしてC1を作成します。しきい値（この場合は１とした）より低いものを無視して、L1を作ります。L1の要素のすべての組み合わせからC2を作ります。ここで、C2のセットで１つ減らした要素( {1 2}であれば{1}と{2}が) L1に入っていない場合、C2の要素としてカウントは出来ません。C2作成に当たりその例はありませんでした。ただC3でその事例が発生します。

C2からスキャンして、先程と同様にしきい値より下のものを削除しL2をつくります。以下同様にC3をつくります。先に説明したとおり、C3の部分集合がL2に含まれていない場合は、その部分集合は入れてはいけません。そのため、{2 3 5}のみが候補として残ります。

さて、Supportさえ出てしまえば、Confidenceを算出することが出来ます。Aprioriアルゴリズムの問題点はメモリです。100個のアイテムから候補を作成するのに2の100乗の候補が必要になり、メモリを圧迫するうえ、データのスキャンにも時間が必要となります。

参考文献

Apriori Algorithm (Python 3.0)

おすすめの記事

投稿者: 等々力 康弘

画像処理エンジニア。組み込みソフト出身。 株式会社モルフォにてR&D部門、主に機械学習業務に携わり、顔認識＆顔検出のアルゴリズム開発に従事。国内特許数件、国際特許１件。 モルフォ社退社後、株式会社Dynaptico創業（CEO)。アメリカ人、スウェーデン人と３名とフードデリバリーサイトmaishoku.comを立ち上げる。社長業の他、開発業務においてバックグラウンド関連全般(Djangoを用いいたバックエンドサーバ＆APIサーバーの作成、 リバースプロキシなどの負荷分散サーバ関連、OCRプログラムの作成、CISCOルータの管理, 、seleniumを用いたテストサーバーの構築、Androidアプリの開発等々）に携わる。 2019年DynapticoのCEOを辞職。 2020年2月にComputer Scienceに特化した株式会社OctOpt創業。 OSはUbuntu。Appleが苦手。Swiftのバージョンアップ対応とか死ぬほど嫌い。 Python/C++/C Twitter: @rocky_house シフト自動調整スケジュールサイトをVue.js+graphene djangoで構築. https://www.allshifter.com

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です