LDAについて

LDAとはLinear discriminant analysisの略で、日本語では線形判別分析と呼ばれています。コンピュータサイエンスでは様々なところで（例えば画像処理でも顔認識など）よく使われ、とてもポピュラーな技術です。

LDAの目的は「クラス内分散とクラス間分散を最大化する」ということにあります。（補足：クラス内、外分散は英語でwithin, betweenと呼ばれている)。結果として、散布図の空間に超平面を引いてデータ群を分離するのです。（超平面に関してはSVMのコラムを確認ください)

例えば、A、B,Cの３つのクラスがあったとします。目的は、３つのクラスをできるだけ遠くにし（クラス間分散最大）、それぞれのクラス間はできるだけ良くまとまっている（クラス内分散は最小）の集合にする事を目的としています。

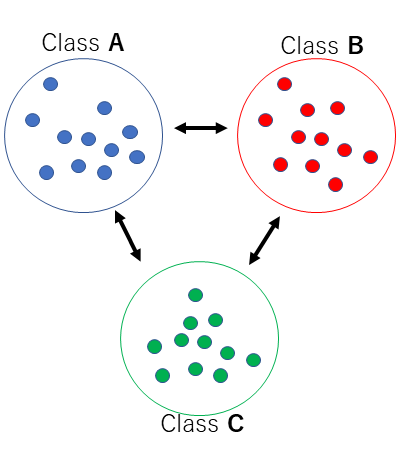
クラス内の分散はなるべく低いほうがいいため、中心（平均、重心）に寄って行きます。クラス間分散はおおきくするため、なるべく遠くへ遠くへ、まんべんなく散らします。

LDAをどうやるかの前に、簡単に予備知識として平均と分散について話した後、具体的な操作を説明することにします。LDAは非常にある意味難しく、分散、平均、擬似行列、PCAなど分かっていなければなりません。一度に覚えようというのは無理なので、じっくりと接して感覚を掴んでください。

平均と分散について

　平均についてはいいとは思いますが、式で説明いたします。以下が平均の式です。全ての数を足しあわせその数で割っているだけの式です。

\mu=\frac{1}{n}\sum_{i=1}^{n}x_i

続いて分散の式ですが、平均からどれだけ散っているか、を表す量です。その散らばり量を表すために、先程求めた平均値との差分をとり、自乗してすべての数の分だけ足しこみます。そして、総数で割ります。（いえば、差分の自乗の平均です）

何故自乗するかというと、平均との差分であるためにマイナスになるケースがあるため、マイナスをなくす目的もそうですが、自乗することで差分が大きい場合にペナルティを与えることが出来ます。分散がどういうものかについて、解るには結構時間がかかります。様々な数字に慣れ親しんで感覚を掴んでいきましょう。（結局はどれだけ散っているか図るためだけの材料です。平均よりも分散が高ければ散っているという感じを受けてください。）

S^2 = \frac{1}{n} \sum_{i=1}{n} (x_i-\mu)^2

分散は平均からの誤差を表しています。データ群は、平均からどれだけ「平均して」はなれているか、という指標です。分散が０なら全然離れていない。平均よりも分散値が大きいなら、結構ばらついているというような、データのまとまり具合がわかります。

LDA

今たくさんのデータがあり、それぞれのデータにはC1とC2のどちらかのラベルがはられていると仮定します。LDAではクラス内分散とクラス間分散を求めなければなりません。まず二つクラスの場合の求め方について説明します。　その後多クラスについて拡張します。

クラス内分散の求め方

今二つクラスがあり、まずは上記式を使ってそれぞれのクラスごとの分散を求めます。ここではその分散の値をss1, ss2とします。そこからクラス内分散を求めるには、単純に

ss_{within} = ss_1 * 0.5 + ss_2 * 0.5

とするだけです。ただし、注意して欲しいのですが、上記の式を使えるのは、ss1 と ss2 の要素数が同じの場合です。（SS1は１０個、SS2も１０個など）クラス内の要素数が違う場合、重みを等しくおくのは適切ではありません。要素数が違う場合（実際にはこの場合がほとんど）、加重平均で割ります。

正しいクラス内分散（それぞれのクラス内の分散の平均）

weight_1 = w_1*(w_1 + w_2) \\ weight_2 = w_2*(w_1 + w_2)\\ ss_{within}= weight_1 * ss_1 + weight_2 * ss_2\\　

ss1, ss2はそれぞれクラス内で求めた分散です。クラス内分散が求まりました。意外と簡単です。

クラス間分散の求め方

続いて、クラス間分散を求めます。（クラス同士の離れ具合を計算する。）まず、クラスを全部すっぱ抜いて、要素全ての平均を求めます。これをAVRとします。

これでクラス間分散を求める材料は揃いました。クラスの平均から全体の平均を引算する。（今二つのクラスがありますので、AVR1, AVR2と置きましょう。）

ss_{between} = ( weight_1 \times (AVR_1-AVR)^2 + weight_2 \times (AVR_2 - AVR )^2) 

weight1, weight2についてはクラス内分散を求めたときと同じ値を使います。

判別に用いる、マハラノビス汎距離

判別にはどうすればよいでしょうか？答えはマハラノビス距離を用います。マハラノビス距離で例えばあるｘというものがAとBのどちらかに属しているのかということを知るのには以下のような指標を用います。

|(x-A群の平均値)/A群の標準偏差|　と　|(x-B群の平均値)/B群の標準偏差|

の小さい方に属させるます。つまり、（データを分散によって標準化、これがマハラノビス汎距離の考え方です。）

多クラスにおいてのクラス間分散＆クラス内分散の求め方

他クラスの場合を考えます。また線形判別分析を行うために共分散行列として求めます。LDAのおさらいですが、今、特別な空間において、

最もクラス間の分散が高く、そして、クラス内同士の分散が低くなるようにしたい。

これがLDAの本質です。クラスに分類されるある集合が、どのように写像すればクラス間が最小、クラス間が最大になるのかを考えるのです。

LDAを行うためには、クラス内分散の共分散行列を求める必要があります。求めるには、クラスごとに共分散行列を作り、それを足しあわせてクラス数で割ります。共分散の詳しい求め方についてはPCAのコラムを参考にしてください。上記内容を数式で表すと以下になります。

\sum_W = \frac{\sum_{i=1}^C n_i \sum_{x\in C_i} (x-avr_i)(x-avr_i)^T}{\sum_{i=1}^C n_i}

\sum_W の共分散行列を表しています。２クラス問題の時に考えたときのように、分母ですが、２クラスの時と同様、加重平均で割っています。

クラス間分散も同様に求めます。以下のようになります。

\sum_B = \frac{\sum_{x\in C_i} n_i(avr_i-AVR)(avr_i-AVR)^T}{\sum_{i=1}^C n_i}

AVRは全体の平均を表しています。avri は各クラスの平均です。　よく見ると、２クラスの時を拡張しただけであることに気づくと思います。（共分散行列を作るために転置したベクトルをかけているところも違いますが）

Σ_W とΣ_Bが求まれば準備終了です。

以下を最大化したいような行列Aを求める、という事を行います。

ret = \argmax( \frac{A^T \sum_B A}{A^T \sum_WA })

argmax( その値が最大となるような値 )を取ってやります。上記のretはフィッシャーの判別比とも言われます。判別比を最大化できるような行列Aはどうやっても求まるのでしょうか。

なぜそうなるかを話すと、長くなるので端折りますが、結果的には以下に対して、固有値分解を求めれば、求めたいベクトルAが求まります。（導出に関しては、やや話がそれるので詳しくは説明しません。ラグランジュの未定乗数法を使うのですが、気になる方は参考文献[2],[3]をご参照ください）

\sum_W^{-1}\sum_B

ところが \sum_Wの逆行列ですが、ランクが足りなくて求まらない場合があります。その際はランク落ちを考慮するため、擬似逆行列を用います。擬似逆行列とは、ランク落ちなどに対処するため擬似的な逆行列を作成する操作です。

Aが求まればあとは、それを用いるだけです。Aは固有ベクトルとしていくつか出てきます。固有値が高い順に並べます。適当な所で打ち切りにします。 その固有値に対応した固有ベクトルを用いて判別します。

特定のｘに対して、出てきた固有ベクトルで変換してやります。そして、その変換したベクトルがそれぞれのクラスのどれに近いかを算出します。算出にはマハラノビス汎距離を用いるのです。

顔画像でLDA

Python2での実装例を紹介します。顔画像を用いてLDAします。左向き、右向き、正面の画像を用意して、他クラス分類を実施します。

def M( array ):
    return numpy.matrix( arrray )
def LDA():
    density_matrix = []
    FACE_X = 64
    FACE_Y = 64
    SIZE = FACE_X * FACE_Y
    class_imgs = [glob.glob( "./left/*.jpg" ), glob.glob( "./front/*.jpg" ), glob.glob( "./right/*.jpg" )]
    # 1st step we calculate each_class_avr, overall_avr,
    class_avrs = []
    avr = numpy.array( [0] * FACE_X * FACE_Y )
    cnt = 0
    for imgs in class_imgs:
        s = numpy.array( [0] * FACE_X * FACE_Y )
        for img_path in imgs:
            data = numpy.array( get_density_vector( img_path, FACE_X, FACE_Y ) )
            s += data
            avr += data
            cnt += 1
        s /= float( len( imgs ) )
        class_avrs.append( s )
    avr /= float( cnt )
    print 'step1 ==> done'
    
    # 2nd. within
    sigma_w = M(numpy.zeros( ( SIZE * SIZE ) ).reshape( (SIZE, SIZE ) ))
    for c_avr, imgs in zip( class_avrs, class_imgs ):
        # class co-matrix
        sigma_wi = M(numpy.zeros( ( SIZE * SIZE ) ).reshape( (SIZE, SIZE ) ))
        for img_path in imgs:
            data = numpy.array( get_density_vector( img_path, FACE_X, FACE_Y ) )
            mat = data - c_avr
            sigma_wi += M(mat.reshape( (len( mat ), 1 ) )) * M(mat)
        sigma_w += sigma_wi / float( len( imgs ) )
    print 'step2 ==> done'
    
    # 2nd between
    sigma_b = M(numpy.zeros( ( SIZE * SIZE ) ).reshape( (SIZE, SIZE ) ))
    for c_avr in class_avrs:
        mat = c_avr - avr
        sigma_b += M(mat.reshape( ( len( mat ), 1 ))) * M(mat)
    
    print 'step3 ==> done'
    print sigma_w.shape
    print sigma_b.shape
    sigma_w_inv = M(numpy.linalg.pinv( sigma_w ) )
    print sigma_w_inv.shape
    print sigma_w * sigma_w_inv
    
    lam, vec = numpy.linalg.eigh( sigma_w_inv * sigma_b )
    ans = zip( lam, vec.T )
    ans.reverse()
    print 'step4 ==> Done'
 

参考文献

1. https://ja.wikipedia.org/wiki/%E5%88%A4%E5%88%A5%E5%88%86%E6%9E%90
2. https://axa.biopapyrus.jp/machine-learning/preprocessing/lda.html
3. https://www.iwanttobeacat.com/entry/2018/05/26/203825

おすすめ記事

1. 主成分分析(PCA)
2. 単純ベイズ分類器(Naive Bayes Classifier )
3. 特異値分解(SVD)