数量化理論Ⅳ類はMDS,多次元尺度構成法とも呼ばれます。対象物の類似度を測る手法です。
あるアイテムが似ている、似ていないというのを平面上にプロットすることができます。平面上だけでなくても、直線、或いは3次元上でプロットできますが、多くは視覚的にわかりやすい2次元にプロットする例が多いです。なお、「似ている程度」「似 ていない程度」の量のことを数量化理論Ⅳ類では親近性と呼びます。
MDSの説明ですが、以下のドキュメントが非常にわかりやすく書かれています。導出が気になった方は、是非次のドキュメントに目を通してください。
http://www.page.sannet.ne.jp/yo-skmt/MultiEx/No13-15MU-Text02.pdf
女性ファッション雑誌をMDSで可視化
MDSの利用シーンとしての具体例を考えます。例えば女性専門雑誌がいくつかあるとします(VIVI, an anなど)。女性向けファッション雑誌の内容は男性からするとどれも一緒に見えますが、女性から見ればファッションの種類によって雑誌がかわります。では具体的にどの雑誌とどの雑誌が似ているのか、という事を男性が知りたいときにはどうすればいいのでしょうか。(男性は例え本の中身を見てもさっぱりですよね?)
まさにこんなときがMDSの出番と言えるでしょう。MDSを使えば次のようにマッピングできます。
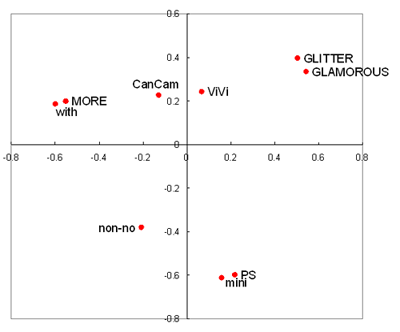
雑誌の中身を見て、これとこれが似ているなど判断しなくてもMDSによりわかりやすく可視化することができます。
その他にも、例えばM1グランプリの採点から、採点者の傾向や、お笑い芸人のタイプなどを可視化出来ます。採点表はネットに公開されているので、興味があったらMDSで実験してみたら面白いかもしれません。
MDSの計算方法
対象物間に「距離」という概念を持ち込む必要があります。対象物間どうしの「距離」の概念を何らかの方法で定義できれば、 固有値分解を実施することでMDSが完了します。距離とは何か、ということを疑問に思った方は距離の公理を参照ください。大抵の場合は馴染み深い距離(ユークリッド距離)を利用するケースが多いです。
ちなみに、どのような行列に対しての固有値分解(あるいは特異値分解)をすることで分析手法の名前が変わってきます[2]
- 相関行列の固有値分解⇒主成分分析or因子分析 (数量化理論III類)
- 分散比行列の固有値分解 ⇒ 判別分析 (数量化理論II類)
- 頻度行列の特異値分解 ⇒コレスポンデンス分析(数量化理論III類)
- 距離行列の固有値分解 ⇒ MDS (数量化理論IV類)
MDSは対象間同士の距離行列さえ求めてしまえば、あとはやる(主成分分解する)だけで可視化できるというのはある意味興味深いです。
距離行列の作成
実際の例で計算をして見ます。今、A,B,Cの三人がいたとして、それぞれの互いにどう思っているかを評価してもらいます。(親近性の調査)
| Aは | Bは | C は | |
| Aのこと | NaN | 3 | 3 |
| B のこと | 4 | NaN | 3 |
| C のこと | 3 | 2 | NaN |
上記のように、互いに評価をしています。なおこの行列を親近性行列と呼びます。
MDSとは、例えば3人を親密な人は距離が近く、そうでない人同士が遠くなるように位置を求めることです。2次元でも、3次元でも考えられますが、計算できる次元数は{対象者−1}次元となります。なお、親近性行列の要素は e_{11}, e_{12}, e_{13}, e_{21} ... e_{32}, e_{33}のように、 e_{ij}として表すことにします。
1次元の直線でA,B,Cの親近性を表現すること考えてみます。A, B, Cのそれぞれの位置をx1, x2, x3とします。ここで、位置x1, x2, x3の制約条件を次のとおりに定めます。
- x1, x2, x3の平均は0
- x1, x2, x3の分散は1
そして関数Qというものを定義します。関数Qは次のような定義です
m=特定の2人の親近性\times 特定の 2人の距離の2乗つまり次のようになります。
m=e_{ij}\times (x_{i} - x_{j})^2全員分のmの総和にマイナスしたものをQとして定義します。
Q=-\sum{ m_k }Qの最大化を行うと、親近性の大きい個体の距離は短く、親近性の小さい個体の距離がなくなるようになります。なお、距離の定義は今回は線分で見るのでユークリッド距離を使いますが対象により変わります。要は距離の公理の「距離」が定義できるものであれば何でも良いです。
さてこれらを用いて計算ですが、細かい導出が坂元保秀教授により大変素晴らしくまとめられています。[1]
数式が多くなるので、結論を書きますと親近性行列から行列Hを定義します。行列Hとはh_{12} = e_{12} + e_{21}という形で、対角線同士を足し合わせる行列となります。対角線の要素[ latex ] e_{11}, e_{22}, e_{33} [/latex]については、e_{11} = -(e_{12}+e_{13}) \times 2 のように、自分意外の行を全て足しこみ、二倍してマイナスにした数字です。以上の操作を図にすると次のとおりです。

行列Hがでたあとは、固有値分解をすることでx1,x2,x3が算出されます。いま、Pythonを用いて行列Hを固有値分解してみましょう。
import numpy as np import math a = [-12, 7, 6] b = [7, -14, 5] c = [ 6, 5, -5] mat = np.array( [ a, b, c ] ) e_value, e_mat = np.linalg.eig( mat ) x1, x2, x3 = e_mat.T[ 0 ] print x1, x2, x3
e_valueは固有値、e_matには固有ベクトルが入っています。e_matに格納されている値がまさにx1, x2, x3となります。それぞれの値は[-0.521333010475 -0.44553760869 -0.727810505167]となっています。
ここで先程の制約条件を思い出してください。平均が0、分散が1ということで定義しました。この条件が合っていることが確認できるかと思います。(厳密には要素数が3ですので、x1, x2, x3にsqrt(3)をそれぞれ掛けた値で分散が1になるのですが、スケーリングするということだけですので気にしなくて構いません。)
もし直線でなく平面でプロットしたい場合は固有ベクトルの1行目と2行目を使います。今一行目でx1, x2, x3としましたが、2行目をy1, y2, y3としてプロットすればよいだけです。3次元の際は、3行目をzとして利用します。
参考文献
[1] http://www.page.sannet.ne.jp/yo-skmt/MultiEx/No13-15MU-Text02.pdf
[2]https://www.nikkei-r.co.jp/glossary/id=1605