はじめに
ページランクの仕組み 、アルゴリズムを意外と知らない人は多いと思います。ページランクアルゴリズムはGoogleの創業者であるLawrence Page とSergey Brinにより考案されました。今や世界を支えていると言われる検索エンジンアルゴリズムはとてもシンプルな式でした。
PR(webPage_x) = (1-d) + d \times (\frac{ PR(webPage_1)}{Count(webPage_1)} + ... + \frac{ PR(webPage_n)}{ Count(webPage_n)})PR()はページランクを表します。最初は定まっていないので初期値として全てのページに適当な値を入れますが1を入れるケースが多いです。
dは減衰率でオリジナルの論文では0.85として設定されています。
Count()はWebページが持つリンクの数です。たとえばWebPage1がリンクを10個持っていればC( WebPage1 ) は10となります。
上記式をみると、自分のページランクをリンク数で除算し分け与えているという意味となります。こんな単純なアルゴリズムから世界を変えるほどの技術となっているのは本当に驚きです。
さて実際の計算しページランクがどのように更新されるのか見てみます。
Page Rankを計算してみる
以下のようなページがあったと仮定します。
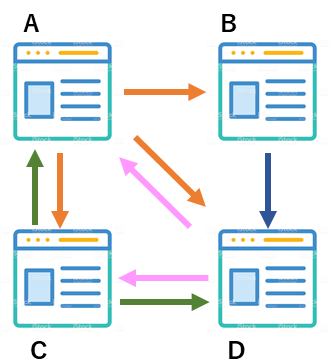
今、4つのウェブページがあり、それぞれリンクを張っています。Aは3つ、Bは1つ、Cは2つ、Dは2つリンクを張っています。このリンクを貼られたという関係を表すと次のようになります
| Aから | B から | C から | D から | |
| Aへ | 0 | 0 | 1 | 1 |
| Bへ | 1 | 0 | 0 | 0 |
| Cへ | 1 | 0 | 0 | 1 |
| Dへ | 1 | 1 | 1 | 0 |
例えば、Aは(B,C,D)にリンクを張っていますので(B,C,D)にそれぞれ1を立てました。
続いて確率モデルの表を先の表から作成します。今Aのリンク数、Count(A)は3です。Aが他のサイト(B,C,D)への分配数はその逆数である1/3ずつが分配されます。上の表をそれぞれのリンク数で除算し,作成された表は次のとおりです。
| Aから | B から | C から | D から | |
| Aへ | 0 | 0 | \frac{1}{2} | \frac{1}{2} |
| Bへ | \frac{1}{3} | 0 | 0 | 0 |
| Cへ | \frac{1}{3} | 0 | 0 | \frac{1}{2} |
| Dへ | \frac{1}{3} | 1 | \frac{1}{2} | 0 |
行列の縦軸に注目すると、合計が必ず1になっていることに気づくと思います。また、マイナスの値が入っておりません。一般的にこうした行列のことを確率行列( column-stochastic matrix)と呼びます。
ページランクベクトルを用意し、先の式に適用していくとページランクが出てきます。今、初期値のページランクを1とします。
PR(A) = 1, PR(B) = 1, PR(C)=1, PR(D)=1
準備がととのったのでページランクを計算します。わかりやすさを重視するために愚直なコード、いわゆるベタ書きコードで表します。実際のプログラムでは、100万ページがあってもエレガントに解けるようなソースコードの書き方を目指してください。
def main():
# PageRank初期値
PR = {'A': 1.0, 'B': 1.0, 'C':1.0, 'D': 1.0 }
# リンク数の逆数(確率)
Prob = {'A': 1/3.0, 'B': 1, 'C':1/2.0, 'D': 1/2.0 }
# 減衰率
d = 0.85
# 10回回す
for i in range( 10 ):
new_PR_A = PR[ 'C' ] * Prob[ 'C' ] + PR[ 'D' ] * Prob[ 'D' ]
new_PR_B = PR[ 'A' ] * Prob[ 'A' ]
new_PR_C = PR[ 'A' ] * Prob[ 'A' ] + PR[ 'D' ] * Prob[ 'D' ]
new_PR_D = PR[ 'A' ] * Prob[ 'A' ] + PR[ 'B' ] * Prob[ 'B' ] + PR[ 'C' ] * Prob[ 'C' ]
PR[ 'A' ] = (1-d) + d * new_PR_A
PR[ 'B' ] = (1-d) + d * new_PR_B
PR[ 'C' ] = (1-d) + d * new_PR_C
PR[ 'D' ] = (1-d) + d * new_PR_D
# 新しい値を出力
print( "%.4f %.4f %.4f %.4f" % (PR[ 'A' ], PR[ 'B' ], PR[ 'C' ], PR[ 'D' ] ) )
if __name__ == '__main__':
main()
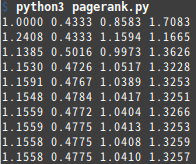
10回ぶん回した結果は次のとおりです。段々と値が安定しているのがわかります。
ページ数や構造がシンプルな例でページランクの計算方法をみてみましたが、実装がシンプルであり、とてもわかり易いアルゴリズムであると思います。ただ、世の中のモデルがこのように単純な問題であるとは限りません。例えばリンクを貼られていないページがあるとどのような問題がでてくるのでしょうか。
Rank Sinks問題
あるページがリンクを全く持っていない問題のことをRank sinks 問題と呼びます。例えば次のようなケースの場合です。
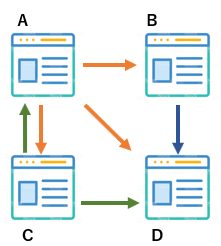
Dが最後になっている場合、Rank Sinksと言われています。流しのシンクのようになっているからです。Dはリンクを持っていないので移動する確率は0であり、周りからページランクをもらうだけです。Dは必然とページランクが上がる一方で、他に配る宛もなく、これは公平ではありません。
この場合はシンクDの移動確率は、全ページ数の逆数を利用することで問題解決を図ります。今(A,B,C,D)と総ページ数4ですので1/4がDの移動確率として定義されます。
| Aから | B から | C から | D から | |
| Aへ | 0 | 0 | \frac{1}{2} | \frac{1}{4} |
| Bへ | \frac{1}{3} | 0 | 0 | \frac{1}{4} |
| Cへ | \frac{1}{3} | 0 | 0 | \frac{1}{4} |
| Dへ | \frac{1}{3} | 1 | \frac{1}{2} | \frac{1}{4} |
全ページ数の逆数である理由は、最後にたどり着いたページからランダムに別のページに行く確率は等確率である、という仮定に基づいています。
注意(ページランクのもう一つの式)
ページランクの式としてはNで割る場合もあります。
PR(A) = \frac{(1-d)}{N} + d \times (\frac{ PR(webPage_1)}{Count(webPage_1)} + ... + \frac{ PR(webPage_n)}{ Count(webPage_n)})最初の項目でNという項目が入っただけです。Nはページ数を表しており、先の例であれば4が入ります。この修正された式の理由は全てのページランクの合計は1である、つまり確率モデルとして正しい形を求めた為です。従って本質的な意味の違いはありません。
ところで、PageRankのアルゴリズムはマルコフ連鎖であるといわます。マルコフ連鎖とはざっくりいうと、次の状態は前の状態からのみ決定されるというものです。ページランクのアルゴリズムを観ると分かる通り、一つ前の状態からしか次のページランクは影響をうけません。そのため、マルコフ連鎖を仮定してという言い方がされます。
ページランクの仕組みは理解できましたでしょうか?当サイトが皆さんの知識の工場に役立ってもらえれば幸いです。
参考サイト
- http://home.ie.cuhk.edu.hk/~wkshum/papers/pagerank.pdf
- http://pr.efactory.de/e-pagerank-algorithm.shtml
- https://en.wikipedia.org/wiki/PageRank