投稿者: 等々力 康弘

はじめに

Deep Learning(ディープラーニング）という言葉は、もはや殆どの人が耳にしたことがあると思います。ディープラーニングは何かを調べていくと、今いち何か掴めないという人が多いのではないでしょうか？今回はディープラーニングの１種であるCNN( Convolution Neural Networks)を中心に画像処理を例として ディープラーニングとはなにか、どう学習させていくかを説明いたします。

Deep learningの正体

ディープラーニングはDeep Neural networks(DNN)とも呼ばれており、その正体はニューラルネットワーク（NN）そのものです。ディープラーニングという言葉が流行り始めた際、中身がニューラルネットワークという事を知って、本当に驚きました。というのも、NNはとても古く伝統ある学習アルゴリズムでしたが、ランダムフォレストやSVMの台頭により、誰も利用しない、古い学習アルゴリズムとして扱われていたからです。厳密にはNNとDNNの違いは、特徴量の作成を学習化にとりいれた事でした。今まで画像処理の分野では技術者は頑張って特徴量を作り、その特徴量をNNなどの学習機で学習させていましたが、DNNでは、画像を突っ込めば前段で特徴量を勝手に作ってくれます。（厳密には特徴量を作成するフィルターを作成する。そのフィルターをかませることで特徴量マップを作成する）これは、とても斬新でした。

Forward process

さて、ディープラーニングの一種であるCNNを例にどのようなに学習しているかを説明します。CNNがわかると、DNNの構造がわかり、例えば最近の技術であるDCGANの理解も進みます。

CNNはFowardプロセスとして前段と後段の２つに分けることができます。まずは前段の畳込みとプーリングについて説明します。

前段（ 畳込みとプーリング ）

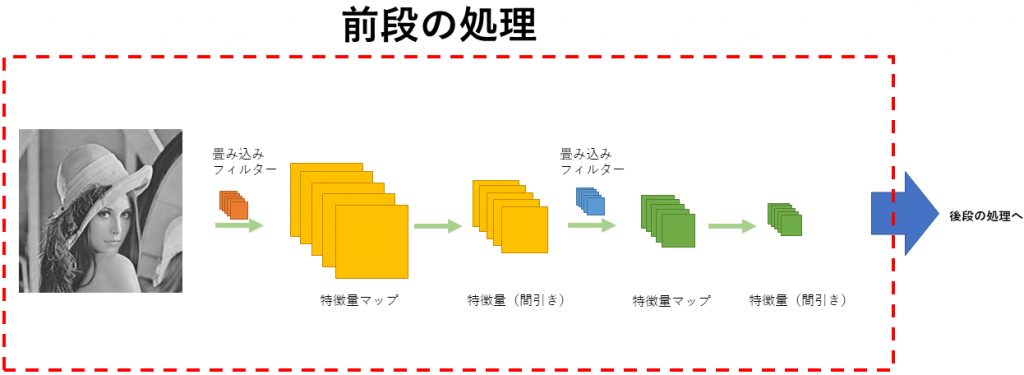
１．畳み込み処理

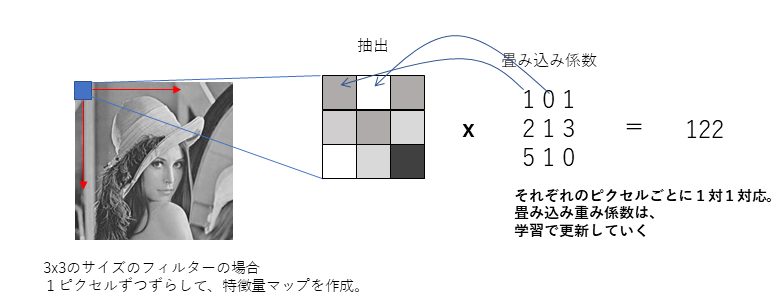
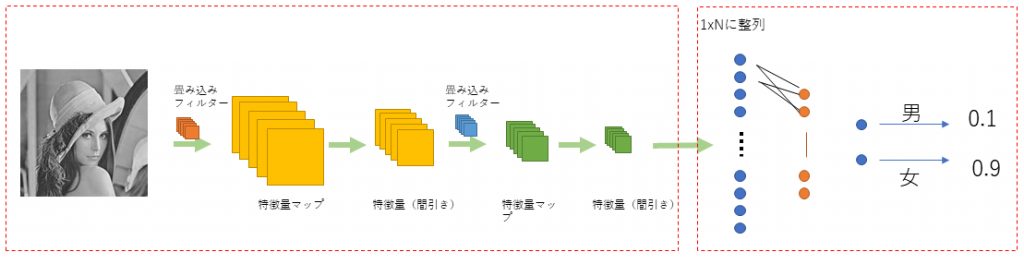
CNNでやっていることは実は単純です。CNNでは、入力画像にフィルターによる畳込み演算をし、それを特徴量マップとして次の層に渡します。この特徴マップづくりが特徴量を自動でつくる、と言われている部分でもあります。CNNは多層であるということを言いましたが、次の層でも、同様に畳込み演算を実施して、更に特徴量マップを作成します。そして次の層へ…ということを繰り返し実施するのです。何層にするかは自分で決めればいいのですが、大体２層くらいで落ち着かせる事が多くあります。

CNNの肝は特徴量マップ作りですが、これは言い換えればフィルター（畳み込みの重み）を学習により自動で求めることにあります。繰り返しフィルターの重みをを更新していく処理により精度を高めていきます。フィルターの更新にはバックプロパゲーション（誤差伝播）により更新していくのですが、こちらは後述します。

なお、畳込み処理ではReLU処理をする場合がほとんどです。ReLUとはmax( 0, x )というただのMAX処理で、畳こみ値がマイナスであれば０にする操作となります。

2.プーリング処理

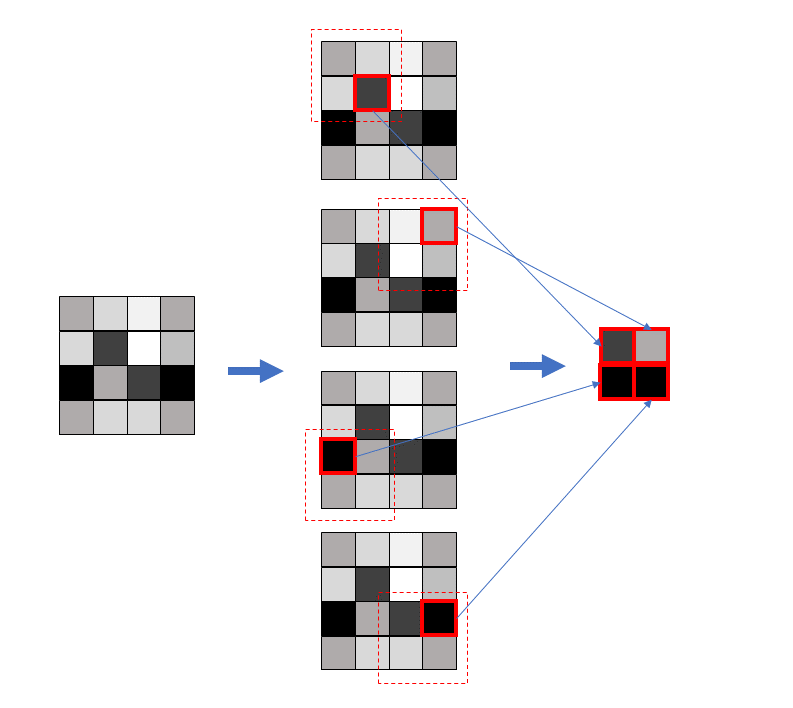
CNNではPoolingという作業（間引き）を行っています。Poolingは特徴量をマップを作った直後（あるいはReLU処理後）に実施します。

最も使われるPooling操作は畳み込み演算後の特徴マップから、ウィンドウの中で最大値だけをとるMaxPoolingです。Poolingを行う最大の目的は次元の削減にあります。またPooling操作は必須ではありません。事実、DCGANなど最近のDNNの一種では行っていません。ただ、伝統的な？CNNでは利用されています。また、至るところでも解説されているので覚えておくといいでしょう。

前段における注意事項

Note 1：入力画像がカラー画像の場合

入力画像がカラー画像のとき、つまりR,G,Bチャンネルが３つあるときですが、フィルターが３次元となります。例えばウィンドウサイズが３ｘ３であれば、RGBを含め３ｘ３ｘ３のフィルターを用意します。このフィルターを適用して、特徴量マップの１つの要素ができます。

Note 2:何枚の特徴量マップを作ればいいのか

各層において、何枚の特徴量マップを作ればいいのかは、自由に決めます。６４，１２８など、霧のいい数字を用いることが多いです。

NOTE 3: 何層作ればいいのか

２層の例が圧倒的に多いですが、こちらも経験的に決めているようです。

後段処理（Classification)

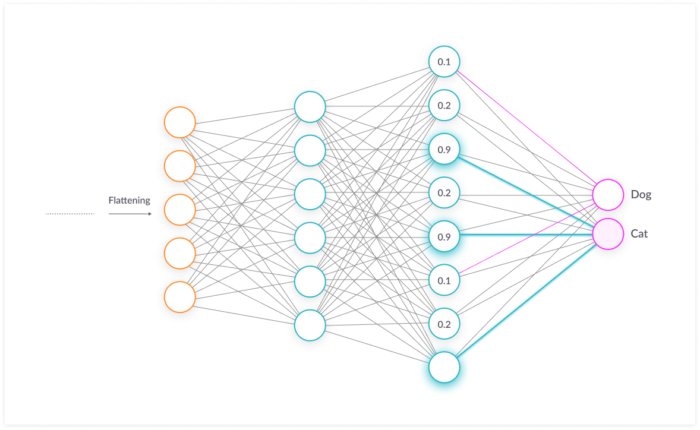
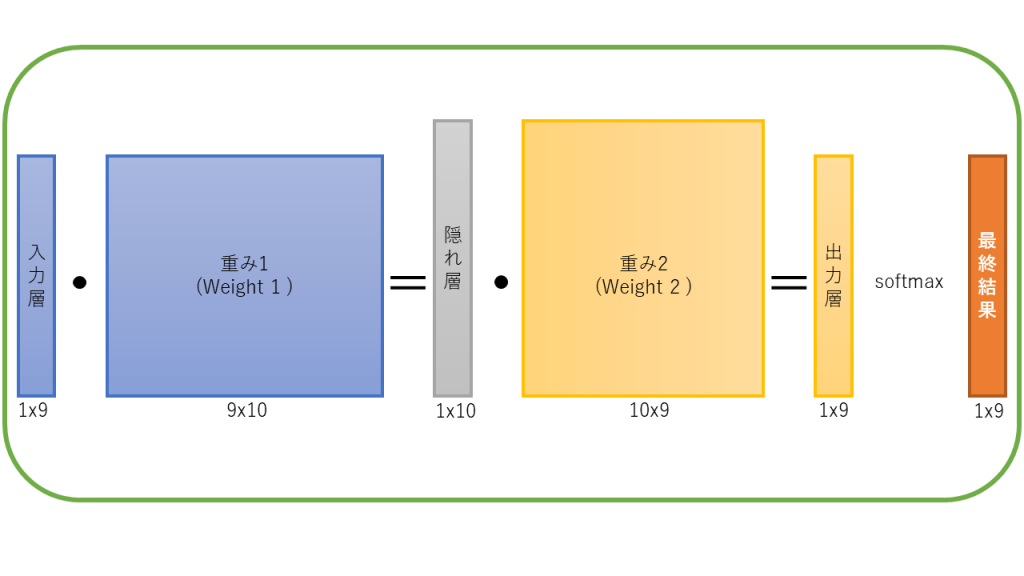
後段処理では、伝統的なニューラルネットワークを行います。例えば、最後に１４ｘ１４の特徴量MAPが３つできたとします（１４ｘ１４ｘ３）。これを１次元にすると５８８次元です（Flattering処理）。これを用いて、普段のNNで使われるテクニックを使い、指定のクラスの次元まで落とし込むのです。SOFTMAXがよく使われています。この方法については、従来のNNそのものであるので割愛します。

Backward process

誤差伝搬はどのようにやるのでしょうか。後段処理についてはNNで今までと変わりません。前段の誤差伝搬処理について解説していきます。

誤差伝搬を行いますが、今までとの逆の操作をしていくことになります。前段処理は次のような流れでした。

画像 –> 特徴量マップ –> ReLU –> MaxPooling

本当は数回特徴量作成とPoolingをやりますが、ここでは簡単に一層で作成したと仮定し説明します。さて、逆操作では以下になります。

d Max Pooling –> d ReLU–>d Convolution(特徴マップ逆操作 )

d Max Pooling

Forward processでのMax Poolingは最大値だけを抽出し、次元を縮小する操作でした。Backward Processでは、次元縮小に利用したフィルターを用いて、後段から来た誤差をもとの大きさにもどしてやります。

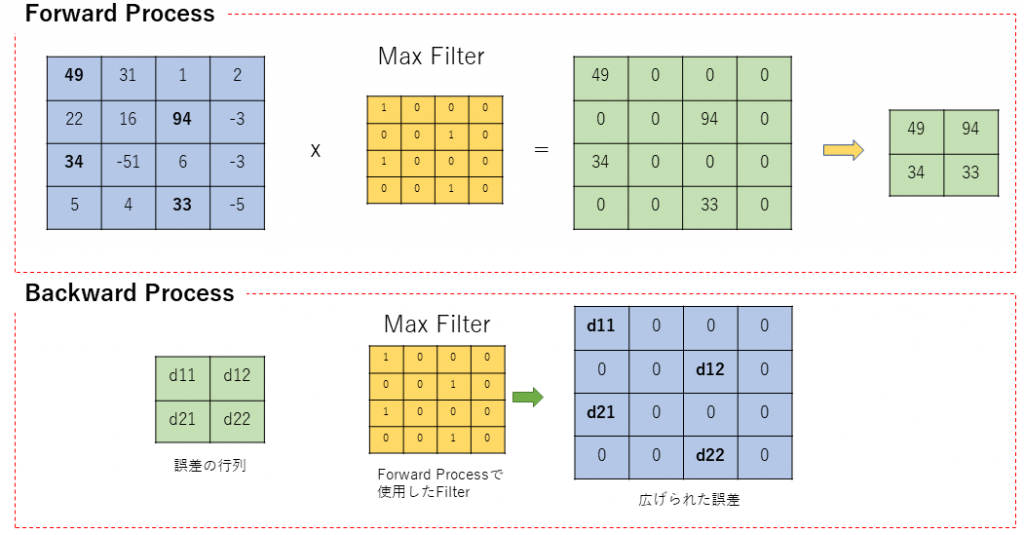
Backword processでは、このMAX Filterを使うので、前段で作ったMAX Filterは保持しておくことが必要です。

d ReLU

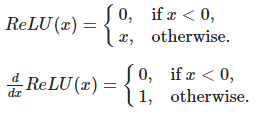
この操作を図示すると次のとおりです。単純に０より上であれば１にする操作となります。

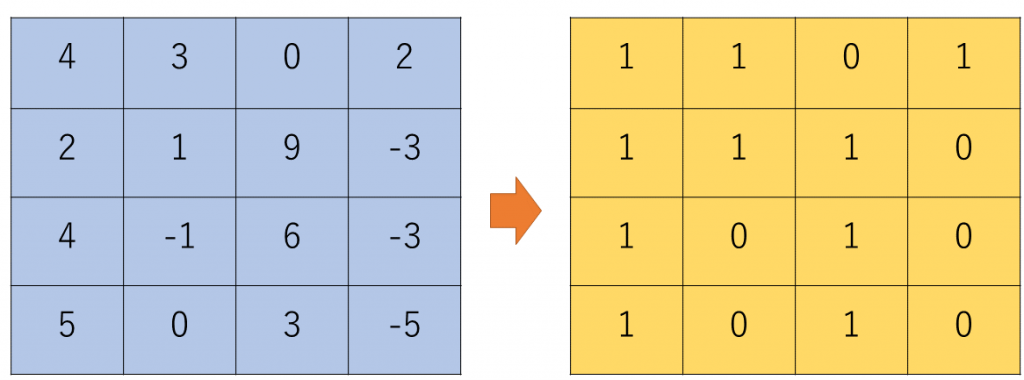
d Convolution

特徴量MAPの作成に利用したフィルターを使い、復元していきます。

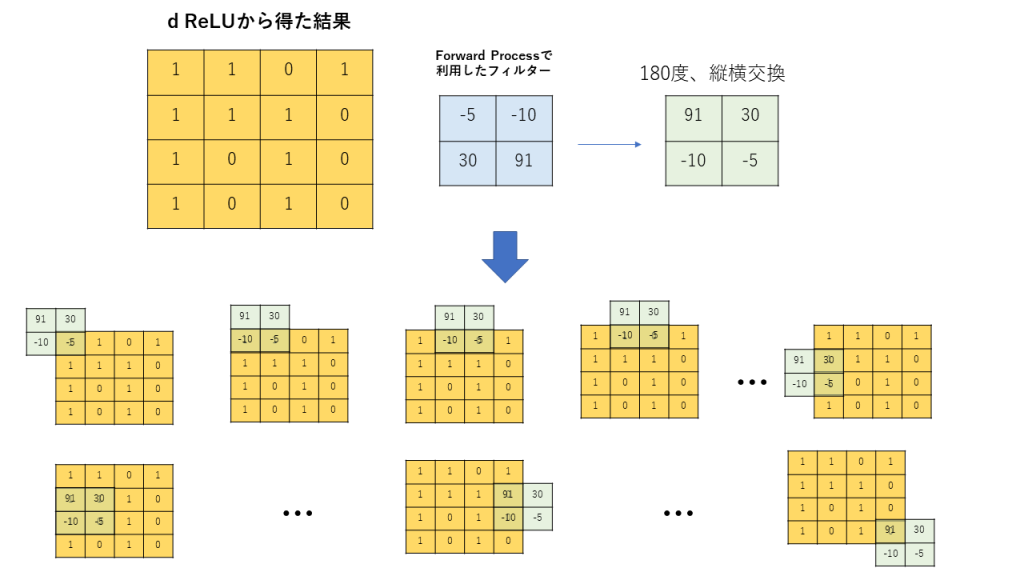
１８０度転置したものが伝搬で使われるのかについてはForward And Backpropagation in Convolutional Neural Network[1]に詳しく述べられていますので、参照ください。参考サイトは英語ですが、わかりやすい数式で述べられているので、興味ある人は読めるはずです。

参考文献

[1] medium.com/@2017csm1006/forward-and-backpropagation-in-convolutional-neural-network-4dfa96d7b37e

https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53

おすすめ記事

• RNN
• 強化学習
• ガボールフィルター

はじめに

Word2Vecは近年で最も注目された技術の一つです。主にNLP( Natural Language Processing:自然言語処理 )の分野の技術なのですが、広告や商品ページなどの推薦エンジン技術として利用されています。実際に楽天などでは本技術を使っているようです[1]。
コンセプトはとてもシンプルです。今回はWord2Vecがどういう技術かをpythonをもとにnumpyを使ったソースコードの実装例をもとに説明します。(gensimなどのライブラリは使いません！）。実際内部でどのような処理が行われているか参考にしてください。

どのようなモデルか

このような構成をしています。すべて本ブログで解説しますので、読み終わる頃にはよくわかります。

Word2Vecは何か

単語をベクトル化する、これをWord2Vecが行います。単語のベクトル化ができることで、四則演算が使えてしまうのです。。

例えば、仮に単語の「神様」：[5, 1, 3]というベクトルで表した場合、「神様」と似ているベクトルを探すこと（例えばコサイン積をとって１に近いものを探すこと）ができます。他にも「神様」:[5,1,3]へ新しく、例えば「海」:[1,2,3]というベクトルを足し込んだ結果を探すと、「リヴァイアサン」:[6,3,6]がヒットするかもしれません。外積をとって直行する言葉を探すなんてこともできそうですね。

その昔、類似度を探す技術と言えば共起行列を用いて探る方法が一般的でした。文章から単語を抽出してともに出現する単語から共起行列を作成してSVDなどで解析し、特徴量空間にマッピングして類似度を算出するのです。ただ、この方法では行列のサイズが大きくなると計算がおいつかなくなる問題がありました。２０１３年にGoogleの研究者がWord2Vecを提案し、業界がざわつきました。

単語をベクトル化することは「word embedding」と呼ばれます。

Word2Vecの実装に向けて

Word2Vecのアルゴリズムは大きく２つあり、違いは次のとおりです。

• Continuous Bag-Of-Words (CBOW)
  • Skip-gramよりも数倍学習が早く、頻出単語に関しては若干の高い精度を誇っている。
• Continuous Skip-gram (SG)
  • 小さい学習データから珍しい単語やフレーズを上手に表現できる。

２つともに近くの単語（ context words ）からの確率分布を用いた手法であります。近傍の単語から新しい単語の類推をしていきます。今回はSG（ Skip-gram ）を説明します。

学習方法

学習データは文章を使います。今回は次のフレーズを元にWord2Vecを説明します。

「Although the world is full of suffering, it is full of the overcoming of it.」
（世界は苦しいことでいっぱいだけれども、それに打ち勝つことでもあふれている。） : マザーテレサ

上記英語フレーズを学習データとします。実践では長い文章を用意します。

さて、Skip-gram では学習にニューラルネットワークを使います。教師データとなるトレーニングデータは単語の近傍の単語（context wordsとよばれる）です。具体的に行きましょう。例えば、先のフレーズの「world」であれば、[Although, the, is, full]がcontext wordsとして学習セットになります。

フレーズ内の、すべての単語に対し同様に学習セットを用意します。たとえば、Althoughの近傍の単語context wordsは[the, world]となります。後述しますがovercomingの近傍ワードは[ of,the, of, it ]ですが、重複は除かれるルールになるので [ of,the, it ] となります。

Vocabulary & One-hot Encoding

Vocabulary

具体的な学習データの作り方ですがVocabulary(ボキャブラリ)を構築し、one-hotエンコーディングを実施する必要があります。

「Vocabulary」とは重複のない単語群のデータです。まずは文章を空白区切りします。

[‘Although’, ‘the’, ‘world’, ‘is’, ‘full’, ‘of’, ‘suffering,’, ‘it’, ‘is’, ‘full’, ‘of’, ‘the’, ‘overcoming’, ‘of’, ‘it’]

そして、重複を除きます。

[‘Although’, ‘the’, ‘world’, ‘is’, ‘full’, ‘of’, ‘suffering,’, ‘it’, ‘overcoming’]

‘it’, ‘is’ , ‘full’ , ‘of’ , ‘the’の重複が取り除かれ１つになり、９次元のデータがとれました。これで「Vocabulary」 が完成しました。

One-hot encoding( One hot vector )

続いてone-hotエンコーディングを行います。図を見るとわかりますが、単純に単語があるところを１にし、それ以外を０にするだけのベクトルを作るという意味です。

One-hot vectorとも呼ばれています。さて、以上で下準備は終わりました。

最初にworldのcontext wordsは「Although, the, is, full」と説明しました。このデータはone-hotベクトルで表現すると　[list([0,0,1,0,0,0,0,0,0]), list( [ 1,0,0,0,0,0,0,0,0 ], [ 0,1,0,0,0,0,0,0,0 ], [ 0,0,0,1,0,0,0,0,0 ], [ 0,0,0,0,1,0,0,0,0 ] ) ]というペアになります。

Training

学習の流れですが、学習の全体像は次のとおりとなります。

Word2Vecでは、ニューラルネットによる学習において、上記のうち、２つの重みマトリックス(W1, W2)を更新していきます。（その方法は次の章で記載します。）

学習終了後ですが、使われるものは重み行列W1です。実はこれが特徴量行列となっています。例えば、”although”[ 1,0,0,0,0,0,0,0,0]があったとして、これと学習後の重み行列W1をかけ合わせて出てきたものが”although”の特徴量ベクトルです。実際には掛け合わせると言っても one-hotベクトル内で １が立っている行をW1から抜き出すという操作になります。

さて、では具体的にどのようにWord2Vecでは学習されているか解説します。

Trainig – Forward pass

まず、一番最初のプロセスとして行列W1,W2はランダムな0-1の範囲で初期化をしておきます。そしてニューラルネットのforward関数としては次の関数を使うことになります。

def forward_pass(onehot_input, w1, w2):
    h = np.dot(w1.T, onehot_input)
    u = np.dot(w2.T, h)
    y = self.softmax(u)
    return y, h, u

onehot_inputは先の例で言うところの [0,0,1,0,0,0,0,0,0] (入力単語 worldのone hot表現)です。重み行列W1とonehot_inputでドット積を実行してHiddenベクトルh(隠れ層)が求められます。続いて、重み行列W2とHiddenベクトルhでドット積を実行し、出力ベクトルuを算出しsoftmax関数をかけて予測値ベクトル yを算出します。

結局のところforward_pass関数におけるリターンバリューとしては[予測値ベクトル y、Hiddenベクトルh、出力層ベクトルu]の３つを得ます。 softmax関数により必ず値が0〜1の範囲になります。

def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)

Training- Error

forward_pass関数の結果から予測ベクトルyが返ってきました。このｙベクトルの値はsoftmax関数を噛ましているので必ず0-1の範囲に収まっています。さて今、次の予測ベクトルyが返ってきたとします。

y = [0.888, 0.801, 0.766, 0.552, 0.659, 0.371, 0.517, 0.087, 0.212]

ここで、出力すべきであった 「although, the, is, full」のone-hotベクトル[ 1,0,0,0,0,0,0,0,0 ], [ 0,1,0,0,0,0,0,0,0 ], [ 0,0,0,1,0,0,0,0,0 ], [ 0,0,0,0,1,0,0,0,0 ] それぞれと 予測ベクトルyの差分を取ります。期待された結果からどれだけ間違えたかを差分として求めるのです。具体的に示します。

こうして出来た、それぞれの単語で求められたエラーベクトルをすべて足し込み１つのエラーベクトルをeを作ります。このエラーベクトルeはBack Propagation処理で利用し、重み行列を更新していきます。

Training- BackPropagation

ニューラルネットワークでおなじみのバックプロパゲーション（誤差逆伝播）を行います。目的はエラーベクトルeを利用して重み行列(W1, W2)を更新することにあります。

具体的な流れは次のとおりです。

1. Hidden ベクトルhとErrorベクトルeで外積を取り、重み行列w2に対する差分行列dW2を作成します。
2. 重み行列W2とErrorベクトルeで内積を取り、ベクトルmを作ります。入力ベクトルonehot_inputとベクトルmで外積を取り、重み行列w1に対する差分行列dW1を作成します。

それぞれの重み行列W1, W2から、 それぞれ差分行列dW1 *学習率 ,dW2 *学習率を引き、新しい重み行列を得ます。学習率は1%くらいに設定しておきます。

learning_ratio = 0.01
def backprop( w1, w2, e, h, x ):
    dW2 = np.outer(h, e)
    dW1 = np.outer(x, np.dot(w2, e.T))
    # 重みの更新
    w1 = w1 - (learning_ratio * dW1)
    w2 = w2 - (learning_ratio * dW2)

以上で終わりです。これをぶん回していくことで学習していきます。学習後、W1の重み行列が特徴量行列となっています。

Trainig-Loss

損失関数を定義し、学習進み具合をチェックできます。損失関数は実際に学習作業と関係ありませんが、ぶん回す回数（エポック数）を決める上で、発散したりしていないか、きちんと収束しているかを確認する上で重要となります。

損失関数は2つの部分で構成されています。１つめは出力層のすべての要素の合計、の負の値です（softmaxの前）。 2 つめは、近傍の数であるcontext_wordsの数と、出力層のすべての要素（指数関数の後）の合計のログの乗算です。

loss += -np.sum(u) + len(context) * np.log(np.sum(np.exp(u)))

類似語の探索

特徴量ベクトルは、最初に説明したとおりone-hotベクトルと学習後の重み行列W1とのドット積によりもとまります。特徴量ベクトルを取得したら、後は、四則演算となります。例えば類似ワードは内積値が１日買い物となります。ベクトル同士の四則演算をして、得た結果かから色々と考えてみると面白いかと思います。

参考文献

https://towardsdatascience.com/an-implementation-guide-to-word2vec-using-numpy-and-google-sheets-13445eebd281

おすすめ記事

• 強化学習( Reinforcement Learning )
• 再帰型ニューラルネットワーク（RNN)
• ディープラーニング (Deep Learning:CNN )